1.
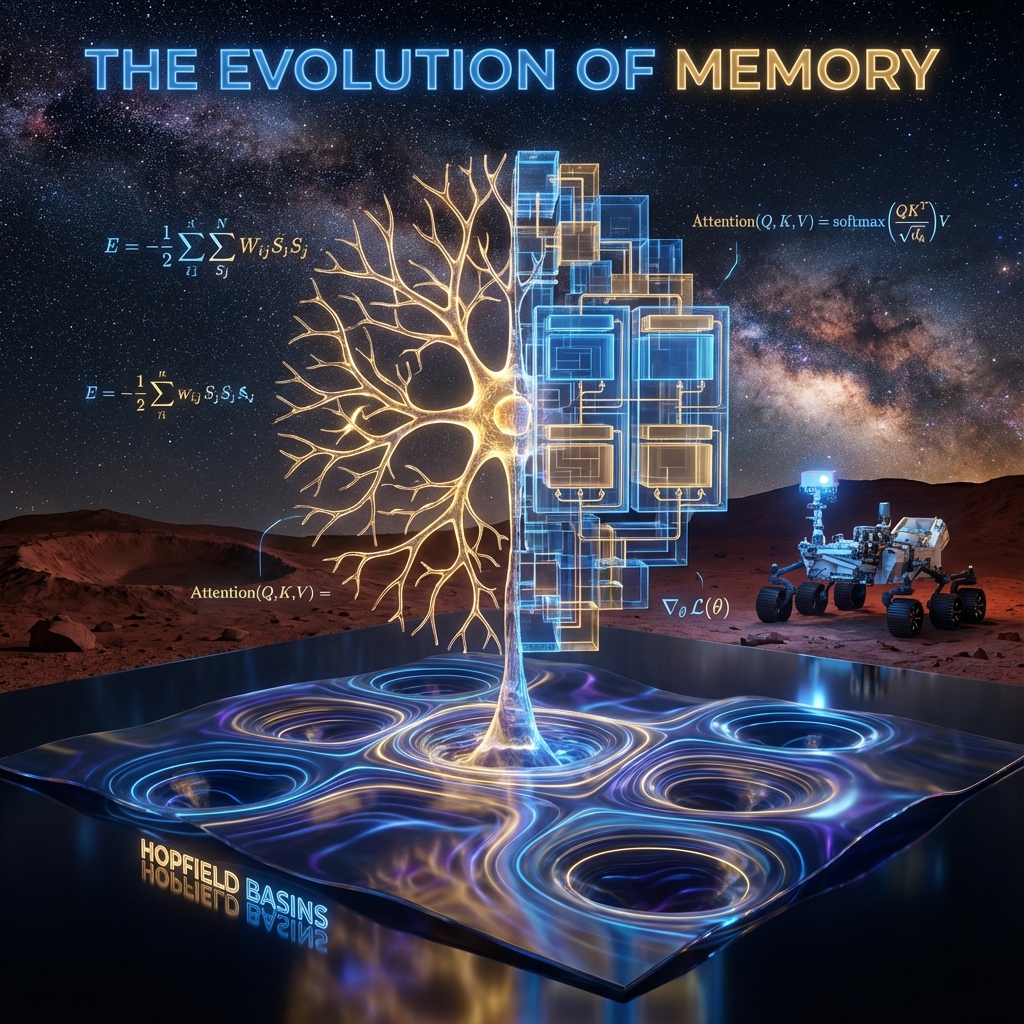
Yapay zeka ve nöromorfik hesaplama alanındaki son on yıllık gelişmeler, klasik “ilişkisel bellek” (associative memory) kavramının yeniden doğuşuna tanıklık etmektedir. 1982 yılında John Hopfield tarafından spin camları (spin glasses) fiziğinden esinlenerek ortaya konan klasik Hopfield Ağları, biyolojik belleğin matematiksel bir modelini sunmuş olsa da, depolama kapasitesindeki lineer sınırlar ($0.14N$) nedeniyle modern veri setleri için yetersiz kalmıştır. Ancak, Modern Hopfield Ağları (MHN) veya diğer adıyla Yoğun İlişkisel Bellekler (Dense Associative Memories – DAM) olarak adlandırılan yeni nesil mimariler, bu kısıtlamaları temelden yıkmıştır. Enerji fonksiyonunun karesel formdan yüksek dereceli polinomlara veya üstel fonksiyonlara dönüştürülmesiyle, bu ağlar süper-lineer ve hatta üstel veri depolama kapasitelerine ulaşmıştır.1
Bu rapor, Modern Hopfield Ağları’nın teorik temellerini, termodinamik özelliklerini ve günümüzün en güçlü yapay zeka mimarisi olan Transformer modelleriyle (örneğin GPT, BERT) olan şaşırtıcı matematiksel eşdeğerliğini en ince ayrıntısına kadar incelemektedir. Analizlerimiz, Modern Hopfield Ağları’nın güncelleme kuralının, Transformer’lardaki Öz-Dikkat (Self-Attention) mekanizması ile birebir aynı olduğunu göstermektedir.3 Ayrıca, bu ağların çekişmeli (adversarial) saldırılara karşı standart derin ağlardan çok daha dayanıklı olduğu, NASA gibi kritik görev sistemleri için hayati önem taşıyan bir “doğal gürültü filtresi” görevi gördüğü ortaya konmuştur.5 Rapor, bu teknolojilerin immünoloji, malzeme bilimi ve otonom sistemlerdeki uygulamalarını da kapsamlı bir şekilde ele almaktadır.
Şu yazılar ilginizi çekebilir.
- Büyük Dil Modellerinin İnşası, Bilişsel Mimariler ve Sub-Sembolik Yapay Zeka
- Gelişmiş Hesaplamalı Mimariler ve Algoritmik Verimlilik: Temellerden Nöromorfik Ölçekleme Yasalarına
- Von Neumann Darboğazı, Transformer Paradigmasının Sınırları ve Uzay Havacılığı Hesaplamasının Geleceği
2. Giriş ve Tarihsel Bağlam: İstatistiksel Fizikten Sinirsel Hesaplamaya
Modern Hopfield Ağları’nın (MHN) getirdiği devrimi tam olarak kavrayabilmek için, öncelikle klasik öncüllerinin dayandığı fiziksel prensipleri ve karşılaştıkları temel darboğazları derinlemesine analiz etmek gerekmektedir. Sinir ağları literatürü ile istatistiksel mekanik arasındaki bu köprü, belleğin “enerji minimizasyonu” olarak modellenmesine dayanır.
2.1 Klasik İlişkisel Bellek Paradigması
Klasik Hopfield Ağı, her biri $V_i$ potansiyeline sahip $N$ adet nörondan oluşan tekrarlayan (recurrent) bir yapıdır. John Hopfield’ın 1982 yılındaki ufuk açıcı çalışması, nöronların kolektif davranışının, manyetik sistemlerdeki “spin” etkileşimlerine benzediğini öne sürmüştür.7 Bu modelde nöronlar ikili (binary) durumlara sahiptir: $\xi_i \in \{-1, +1\}$. Ağın dinamiği, sistemin toplam enerjisini (Lyapunov fonksiyonu) minimize edecek şekilde evrilir. Enerji fonksiyonu şu şekilde tanımlanır:
$$E = -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N w_{ij} \xi_i \xi_j + \sum_{i=1}^N \theta_i \xi_i$$
Burada $w_{ij}$, $i$. ve $j$. nöron arasındaki sinaptik ağırlığı, $\theta_i$ ise eşik değerini temsil eder. Bellek, bu enerji peyzajındaki (energy landscape) “çukurlar” veya yerel minimumlar olarak kodlanır. Sisteme gürültülü veya eksik bir girdi (örneğin bir astronotun yüzünün yarısı) verildiğinde, ağın dinamikleri bu girdiyi enerji yüzeyinden aşağıya doğru yuvarlayarak en yakın yerel minimuma, yani saklanan orijinal anıya (tam yüz görüntüsü) ulaştırır.
Öğrenme işlemi, biyolojik olarak kabul gören Hebbian kuralı ile gerçekleşir: “Birlikte ateşlenen nöronlar, birbirine bağlanır.” $M$ adet örüntü ($x^\mu$) saklanmak istendiğinde, ağırlık matrisi bu örüntülerin dış çarpımlarının toplamı olarak hesaplanır:
$$w_{ij} = \frac{1}{N} \sum_{\mu=1}^M x_i^\mu x_j^\mu$$
Bu basit kural, nöronlar arasındaki korelasyonu ağırlıklara kodlayarak, desenlerin hatırlanmasını sağlar.
2.2 Kapasite Krizi ve Karışıklık Gürültüsü
Klasik modelin en büyük zayıflığı, depolama kapasitesinin son derece sınırlı olmasıdır. Amit, Gutfreund ve Sompolinsky tarafından yapılan titiz istatistiksel mekanik analizleri, ağın hatasız bir şekilde hatırlayabileceği maksimum desen sayısının ($M_{max}$) nöron sayısı ($N$) ile lineer bir ilişki içinde olduğunu kanıtlamıştır.8 Kritik kapasite sınırı yaklaşık olarak şöyledir:
$$M_{max} \approx 0.14 N$$
Bu oran, $N$ nöronlu bir ağın bilgi taşıma potansiyelinin sadece %14’ünün kullanılabileceği anlamına gelir. Bu sınırlamanın temel nedeni “crosstalk” (çapraz konuşma) gürültüsüdür. Ağırlık matrisi $W$, tüm desenlerin süperpozisyonudur. Ağ bir deseni hatırlamaya çalışırken, diğer $M-1$ desenin ağırlık matrisindeki izleri, ana sinyali bozan bir gürültü (parazit) oluşturur. Saklanan desen sayısı arttıkça, bu gürültü terimi baskın hale gelir ve enerji peyzajında “sahte minimumlar” (spurious minima) veya “spin camı durumları” oluşur.7 Sistem, gerçek bir anı yerine, anıların rastgele birleşiminden oluşan ve hiçbir anlam ifade etmeyen “kimera” durumlarına saplanır. Bu durum, klasik Hopfield ağlarının yüksek çözünürlüklü görüntüler veya karmaşık veri setleri için kullanılmasını imkansız kılmıştır.
3. Modern Hopfield Ağlarına Geçiş: Yoğun İlişkisel Bellekler (DAM)
2016 yılında Dmitry Krotov ve John Hopfield, klasik modeldeki bu kapasite darboğazını aşmak için devrim niteliğinde bir öneri sundular: Enerji fonksiyonunu değiştirmek. Klasik modeldeki etkileşimler “ikili”dir (pairwise), yani enerji sadece iki nöronun çarpımına ($\xi_i \xi_j$) bağlıdır. Krotov ve Hopfield, nöronlar arasında çok daha karmaşık, yüksek dereceli etkileşimlerin olduğu sistemleri incelediler. Bu yeni sistemlere Yoğun İlişkisel Bellekler (Dense Associative Memories – DAM) adı verildi.9
3.1 Krotov ve Hopfield’ın Polinom Etkileşim Kuramı
DAM teorisinin temel fikri, enerji fonksiyonundaki doğrusal olmayan (non-linear) etkileşimlerin derecesini artırmaktır. Klasik karesel enerji fonksiyonu yerine, $n \ge 2$ olmak üzere daha yüksek dereceli bir polinom fonksiyonu $F(x) = x^n$ kullanılır. Yeni enerji fonksiyonu şu şekilde ifade edilir:
$$E = – \sum_{\mu=1}^M F\left( \sum_{i=1}^N \xi_i x_i^\mu \right) = – \sum_{\mu=1}^M \left( \langle \xi, x^\mu \rangle \right)^n$$
Burada $\langle \xi, x^\mu \rangle$, ağın o anki durumu ile saklanan $\mu$. desen arasındaki benzerliği (iç çarpımı) gösterir. Bu terimin $n$. kuvvetinin alınması, sistemin dinamiklerini kökten değiştirir. $n$ sayısı büyüdükçe, sistem “en çok benzeyen” desene, diğer desenlere kıyasla çok daha büyük bir enerji avantajı sağlar. Örneğin, bir desenle benzerlik 0.9, diğeriyle 0.5 ise;
- $n=2$ için (Klasik): $0.9^2 = 0.81$, $0.5^2 = 0.25$. Oran $\approx 3.2$.
- $n=20$ için (Modern): $0.9^{20} \approx 0.12$, $0.5^{20} \approx 0.000001$. Oran $\approx 120,000$.
Görüldüğü üzere, yüksek kuvvetler, hedef desenin sinyalini (signal) diğer desenlerin gürültüsüne (crosstalk) göre muazzam ölçüde güçlendirir. Bu sayede, ağın depolama kapasitesi lineer rejimden süper-lineer rejime geçer.1 Polinom enerji fonksiyonu için kapasite şu şekilde ölçeklenir:
$$N_{mem}^{max} \approx \frac{1}{2(2n-3)!!} \frac{N^{n-1}}{\ln(N)}$$
Bu formül, $n$ arttıkça kapasitenin nöron sayısının kuvvetleriyle ($N^2, N^3…$) büyüdüğünü gösterir. Bu, aynı donanım üzerinde milyarlarca kat daha fazla bilginin saklanabilmesi demektir.
3.2 Özellik-Prototip Geçişi ve Enerji Peyzajı
Krotov ve Hopfield’ın çalışmaları, yapay sinir ağlarının çalışma prensiplerine dair derin bir “dualite” (ikilik) ortaya koymuştur.9 Enerji fonksiyonunun kuvveti $n$, ağın bilgiyi nasıl işlediğini belirleyen bir kontrol parametresi gibidir:
- Düşük $n$ (Özellik Eşleştirme Rejimi): $n=2$ durumunda ağ, klasik derin öğrenme modellerinin ilk katmanlarına benzer şekilde çalışır. Girdideki belirli “özellikleri” (feature) tespit eder. Enerji havzaları geniştir ve genel genellemeler yapmaya uygundur.
- Yüksek $n$ (Prototip Rejimi): $n \to \infty$ limitine yaklaşıldığında, ağ bir “prototip belleği”ne dönüşür. Enerji fonksiyonu o kadar dikleşir ki, sistem sadece saklanan desenlere (prototiplere) veya onlara çok yakın varyasyonlara tepki verir. Bu rejimde ağ, “büyükannesini tanıyan nöron” (grandmother cell) mantığıyla çalışır; yani belirli, karmaşık bir bütünü tek bir adımda tanır.
Bu geçiş, modern derin öğrenme ağlarında kullanılan aktivasyon fonksiyonlarıyla (örneğin ReLU – Rectified Linear Unit) doğrudan ilişkilidir. Aslında, Krotov ve Hopfield, ReLU aktivasyon fonksiyonuna sahip bir derin ağın, enerji fonksiyonunda belirli bir polinom derecesine sahip bir DAM’e matematiksel olarak eşdeğer olduğunu göstermiştir.9
3.3 Adversarial (Çekişmeli) Saldırılara Karşı Doğal Dayanıklılık
Modern Hopfield Ağları’nın en çarpıcı özelliklerinden biri, derin öğrenme modellerinin “Aşil topuğu” olarak bilinen çekişmeli örneklere (adversarial examples) karşı gösterdiği üstün dirençtir. Standart derin ağlar (DNN), insan gözünün fark edemeyeceği küçük gürültülerin (perturbation) eklenmesiyle (örneğin bir panda resmine görünmez gürültü eklenip şebeke (gibbon) olarak sınıflandırılması) kolayca kandırılabilir. Bunun nedeni, ReLU tabanlı ağların karar sınırlarının (decision boundary) parça parça doğrusal olması ve gradyanların saldırganlar tarafından kolayca hesaplanabilmesidir.11
Ancak, yüksek dereceli etkileşimlere sahip DAM’ler ($n \ge 20$ veya üstel), enerji peyzajında çok farklı bir topoloji yaratır. Saklanan anıların etrafındaki çekim havzaları son derece dik ve derindir. Bu havzaların dışında kalan bölgeler ise son derece düz (flat plateau) enerji yüzeyleridir.5
- Gradyan Maskeleme: Enerji yüzeyinin düzleşmesi, saldırganın kullanacağı gradyan bilgisini (türevleri) yok eder veya anlamsız hale getirir. FGSM (Fast Gradient Sign Method) veya PGD (Projected Gradient Descent) gibi saldırılar, yön bulamayan pusulalar gibi işlevsiz kalır.
- Anlamsal Bütünlük: Krotov ve Hopfield (2018), yüksek dereceli ağlarda enerji minimumlarının her zaman “anlamsal” (semantic) olduğunu göstermiştir.13 Klasik ağlarda enerji minimumları rastgele gürültü (rubbish examples) olabilirken, MHN’lerde bir minimuma ulaşıldığında bu mutlaka saklanan gerçek bir anıya karşılık gelir.
NASA’nın otonom uzay araçları veya gezegen keşif robotları için bu özellik hayati önem taşır. Sensör verilerine karışabilecek kozmik ışın kaynaklı gürültüler veya kasıtlı sinyal bozucular, DAM tabanlı bir algılama sistemini klasik bir CNN kadar kolay yanıltamaz.
4. Sürekli Modern Hopfield Ağları ve Üstel Enerji Fonksiyonu
Krotov ve Hopfield’ın polinom yaklaşımı kapasiteyi artırsa da, Modern Hopfield Ağları’nın bugünkü popülaritesinin asıl mimarı, 2020 yılında “Hopfield Networks is All You Need” makalesiyle Ramsauer ve ekibidir.3 Bu çalışma, ağı ikili (binary) durumdan sürekli (continuous) duruma taşımış ve enerji fonksiyonunu polinomdan “üstel” (exponential) forma evriltmiştir.
4.1 Sürekli Durum Uzayı ve Log-Sum-Exp Enerjisi
Bu yeni formülasyonda, ağın durumu $\xi$ artık $d$-boyutlu reel sayılar vektörüdür ($\xi \in \mathbb{R}^d$). Saklanan desenler $X = (x_1, x_2, \dots, x_M)$ matrisi olarak ifade edilir. Ramsauer ve ekibi, sürekli durumlar için aşağıdaki enerji fonksiyonunu tanımlamıştır:
$$E = -\text{lse}(\beta, X^T \xi) + \frac{1}{2} \xi^T \xi + C$$
Burada, “lse” (Log-Sum-Exp) fonksiyonu şu şekilde tanımlanır:
$$\text{lse}(\beta, z) = \frac{1}{\beta} \log \left( \sum_{k=1}^M \exp(\beta z_k) \right)$$
- $\beta$ (Ters Sıcaklık): Bu parametre, ağın ne kadar “seçici” olacağını belirler. Yüksek $\beta$ (düşük sıcaklık), ağın sadece en güçlü eşleşmeye odaklanmasını (hard attention) sağlar. Düşük $\beta$ (yüksek sıcaklık), tüm desenlerin ortalamasını almasına (soft attention) neden olur.15
- İkinci Terim ($\frac{1}{2} \xi^T \xi$): Bu karesel terim, durum vektörünün sonsuza gitmesini engelleyen bir regülarizasyon (norm kontrolü) görevi görür.
4.2 Termodinamik Limitler ve Üstel Depolama Kapasitesi
Üstel etkileşim fonksiyonunun ($e^{\langle \xi, x \rangle}$) kullanılması, depolama kapasitesinde teorik olarak ulaşılabilecek en üst sınıra yaklaşılmasını sağlar. Demircigil ve diğerleri (2017) ile Ramsauer ve diğerleri (2020), bu yapının kapasitesinin desenlerin boyutu ile üstel olarak arttığını kanıtlamıştır 1:
$$M_{max} \approx C \cdot b^{\frac{d}{2}}$$
Burada $b > 1$ bir taban ve $C$ bir sabittir. Örneğin, 512 boyutlu bir vektör uzayında, saklanabilecek desen sayısı evrendeki atom sayısını aşabilir. Bu muazzam kapasite, Modern Hopfield Ağları’nı sadece bir “bellek” olmaktan çıkarıp, devasa veritabanları üzerinde anlık sorgulama yapabilen bir “arama motoruna” dönüştürür.
4.3 Güncelleme Kuralı ve Tek Adımda Yakınsama
Sürekli Modern Hopfield Ağı’nın durumunu güncellemek için kullanılan kural, enerji fonksiyonunun gradyanının alınmasıyla (Konkav-Konveks Prosedürü – CCCP) türetilir. Yeni durum $\xi^{new}$ şu formülle hesaplanır:
$$\xi^{new} = X \cdot \text{softmax}(\beta X^T \xi)$$
Bu formülün analizi çok kritik bir sonucu ortaya koyar: Klasik ağlar bir anıyı hatırlamak için defalarca iterasyon (tekrarlama) yapmak zorundayken, Modern Hopfield Ağları genellikle tek bir güncelleme adımında kararlı duruma (fixed point) yakınsar.3 Bu hız, bu katmanların derin öğrenme modellerinin içine (end-to-end) entegre edilmesini mümkün kılan faktördür.
5. Büyük Birleşim: Transformer Mimarileri ve Hopfield Dualitesi
Bilgisayar bilimleri tarihinin belki de en şaşırtıcı keşiflerinden biri, Ramsauer ve ekibinin Modern Hopfield Ağı güncelleme kuralının, günümüz yapay zekasını domine eden Transformer mimarisindeki (ChatGPT, Claude, BERT vb.) Öz-Dikkat (Self-Attention) mekanizması ile matematiksel olarak eşdeğer olduğunu göstermesi olmuştur.3
5.1 “Hopfield Networks is All You Need”: Matematiksel Eşdeğerlik
Transformer mimarisindeki standart dikkat mekanizmasını hatırlayalım. Bir Girdi (Query – $Q$), Anahtar (Key – $K$) ve Değer (Value – $V$) matrisleri üzerinden dikkat çıkışı ($Z$) şöyle hesaplanır:
$$\text{Attention}(Q, K, V) = \text{softmax}\left( \frac{Q K^T}{\sqrt{d_k}} \right) V$$
Şimdi Modern Hopfield güncelleme kuralını ($\xi^{new} = X \cdot \text{softmax}(\beta X^T \xi)$) bu formata uyarlayalım. Eğer Hopfield ağı “hetero-assosiyatif” (yani girdisi ve çıktısı farklı olabilen) bir yapı olarak kurgulanırsa, saklanan desenler ikiye ayrılır: Benzerlik ölçümü için kullanılan desenler ($K$) ve geri çağrılacak içerik ($V$). Ağın o anki durumu ise sorgudur ($Q$).
Eşleşme Tablosu:
| Transformer Bileşeni | Modern Hopfield Ağı Karşılığı | Açıklama |
| Query ($Q$) | Durum Vektörü ($\xi$) | Hatırlanmak istenen ipucu veya sorgu. |
| Key ($K^T$) | Saklanan Desenler Matrisi ($X^T$) | Hafızadaki anıların “adres” veya “etiket” kısımları. |
| Value ($V$) | Saklanan Desenler Matrisi ($X$) | Hafızadaki anıların “içerik” kısımları. |
| Scaling ($\frac{1}{\sqrt{d_k}}$) | Ters Sıcaklık ($\beta$) | Enerji peyzajının dikliğini (seçiciliğini) kontrol eden parametre. |
| Softmax | Enerji Minimizasyonu | LSE enerjisinin türevi sonucu doğal olarak ortaya çıkan fonksiyon. |
5.2 Dikkat Mekanizmasının (Attention) Enerji Tabanlı Yorumu
Bu eşdeğerlik, Transformer modellerinin neden bu kadar başarılı olduğunu fiziksel bir temele oturtur:
- Her Dikkat Kafası (Attention Head) Bir Hopfield Ağıdır: Transformer’ın her katmanındaki her bir kafa, aslında devasa kapasiteye sahip bir ilişkisel bellektir. Gelen token’ları (kelimeleri), eğitim sırasında öğrendiği milyarlarca bağlamsal prototiple karşılaştırır ve en uygun olanı “hatırlar”.
- İçerik Adresli Bellek: Transformer’lar, veriye “adresine” (RAM’deki gibi 0x3F…) göre değil, “içeriğine” (vektör benzerliğine) göre erişir. Bu, Hopfield ağlarının temel özelliğidir.
- Hata Düzeltme: Hopfield dinamikleri, gürültülü girdileri temizleyerek kararlı durumlara çeker. Bu, Transformer’ların bozuk cümleleri tamamlama veya belirsiz bağlamları netleştirme yeteneğini açıklar.
5.3 Meta-Kararlı Durumlar ve Bağlamsal İşleme
Modern Hopfield teorisi, dikkat mekanizmasının davranışlarını “meta-kararlı durumlar” (metastable states) üzerinden açıklar.15
- Eğer $\beta$ çok düşükse, enerji yüzeyi çok düzdür; ağ tüm anıların ortalamasını alır (Global Average Pooling). Bu, cümlenin “genel temasını” anlamaya benzer.
- Eğer $\beta$ yüksekse, enerji yüzeyinde derin çukurlar oluşur; ağ tek bir anıya kilitlenir. Bu, belirli bir isme veya referansa “dikkat kesilmeye” benzer.
Hopfield katmanları, bu $\beta$ parametresini dinamik olarak ayarlayarak veya öğrenerek, ne zaman genele bakacağını, ne zaman detaya odaklanacağını belirleyebilir.
6. Uygulama Alanları ve Kritik Görev Senaryoları
Modern Hopfield Ağları, teorik zarafetlerinin ötesinde, özellikle veri miktarının çok büyük ancak “tanık” (witness) sayısının çok az olduğu problemlerde (Multiple Instance Learning – MIL) rakipsizdir.
6.1 DeepRC: Bağışıklık Sistemi Repertuvar Sınıflandırması
Ramsauer ve ekibi, bu mimariyi biyolojiye uygulayarak DeepRC yöntemini geliştirmiştir.14
- Problem: İnsan bağışıklık sistemi, yaklaşık $300,000$ farklı T-hücresi reseptörü içerir. Bir kişinin belirli bir virüse (örn. CMV veya SARS-CoV-2) sahip olup olmadığını anlamak için bu devasa repertuvarın taranması gerekir. Ancak, hastalığı işaret eden reseptörler (witnesses) sadece birkaçı olabilir. Bu, “samanlıkta iğne aramak”tan farksızdır.
- Hopfield Çözümü: DeepRC, her hastayı bir “çanta” (bag), her reseptörü de bir “örnek” (instance) olarak kabul eder. Bir Modern Hopfield Katmanı, bu yüz binlerce reseptörü belleğine alır. Öğrenilen bir “sorgu” vektörü (hastalık motifi), tüm repertuvarı aynı anda tarar. Üstel kapasite ve keskin dikkat mekanizması (yüksek $\beta$) sayesinde, model 300.000 anlamsız dizi arasından, hastalığı taşıyan tek bir diziyi bulup çıkarabilir.
- Sonuç: DeepRC, klasik yöntemlere (SVM, Max-Pooling) göre çok daha yüksek doğruluk ve hız sağlamıştır. Bu, gelecekteki pandemilerde hızlı tanı kitleri geliştirmek için kritik bir teknolojidir.
6.2 Biyolojik İskileşim: Afinite Olgunlaşması ve Bellek
Modern Hopfield Ağları, biyolojik süreçleri modellemek için de güçlü bir araçtır. Bağışıklık sistemindeki B-hücrelerinin, bir antijene (virüs parçası) en iyi yapışacak antikoru üretmek için geçirdiği mutasyon süreci (Afinite Olgunlaşması), bir enerji peyzajında “en derin çukuru arama” işlemi olarak modellenebilir.20 Antijen, ağa sunulan bir “girdi deseni”, B-hücreleri ise “saklanan anılar”dır. Sistem, enerji (bağlanma enerjisi) minimizasyonu yaparak en uygun antikoru seçer. Bu, bağışıklık sisteminin de aslında bir tür “Yoğun İlişkisel Bellek” olarak çalıştığını gösterir.
Ayrıca, beyindeki Hipokampus bölgesinin anıları yeniden oynatma (replay) ve tamamlama (pattern completion) işlevi, Modern Hopfield dinamikleriyle birebir örtüşür. Eksik bir ipucundan (örn. bir koku) bütün bir anının (mekan, zaman, duygu) canlanması, Hopfield ağlarının çekim havzası dinamiğinin biyolojik karşılığıdır.22
6.3 Uzay ve Havacılık Uygulamaları İçin Gürültü Toleransı
NASA bağlamında, Modern Hopfield Ağları’nın gürültü toleransı hayati önem taşır. Derin uzay iletişiminde veriler kozmik radyasyon, atmosferik bozulmalar veya sensör arızaları nedeniyle sıklıkla bozulur (bit-flip, eksik paketler).
- Otomatik Düzeltme: Bir Hopfield katmanı, gelen bozuk telemetri verisini “en yakın geçerli komut/veri paketine” çeken bir düzeltici (denoiser) olarak kullanılabilir. Üstel kapasite sayesinde, milyonlarca olası komut senaryosu tek bir ağda saklanabilir.
- Güvenli Otonomi: Mars yüzeyindeki bir rover, kamerasındaki toz veya parlama nedeniyle bir krateri yanlış algılayabilir. DAM tabanlı bir vizyon sistemi, “krater prototipine” kilitlenerek, görsel gürültüyü elimine eder ve klasik ağların yapabileceği hatalı sınıflandırmaları (örneğin gölgeyi uçurum sanma) engeller.
7. Teknik Uygulama ve Algoritmik Zorluklar
Modern Hopfield Ağları’nı PyTorch veya TensorFlow gibi kütüphanelerde uygulamak, teorik formüllerin doğrudan yazılmasından daha karmaşıktır. Üstel fonksiyonlar, bilgisayarların sayısal sınırlarını zorlar.
7.1 PyTorch Üzerinde Sayısal Kararlılık (Log-Sum-Exp Trick)
Formüldeki $\exp(\beta X^T \xi)$ terimi, eğer iç çarpım sonucu örneğin $100$ gibi bir değerse, $e^{100}$ sayısı çok büyüktür ($2.6 \times 10^{43}$). Bu durum “floating point overflow” (taşma) hatasına ve NaN (Not a Number) sonuçlarına yol açar. Tersi durumda, çok küçük negatif sayılar “underflow” (sıfıra yuvarlanma) sorunu yaratır.
Bu sorunu çözmek için Log-Sum-Exp (LSE) Trick kullanılır 23:
$$\log \left( \sum_{i} e^{x_i} \right) = a + \log \left( \sum_{i} e^{x_i – a} \right), \quad \text{burada } a = \max(x_i)$$
En büyük değeri ($a$) üslerden çıkarmak, en büyük terimin $e^0=1$ olmasını sağlar ve diğer tüm terimler $e^{\text{negatif}} \le 1$ olur. Bu işlem, sayısal kararlılığı garanti eder ve ağın gradyanlarının düzgün bir şekilde hesaplanmasını sağlar.
7.2 Geri Yayılım (Backpropagation) ve Gradyan Akışı
Hopfield katmanları türevlenebilirdir (differentiable). Enerji fonksiyonunun türevi Softmax olduğu için, bu katmanlar standart geri yayılım (backpropagation) algoritması ile eğitilebilir. Ancak, $\beta$ parametresinin seçimi veya öğrenilmesi kritiktir. Çok yüksek bir $\beta$, gradyanların “kaybolmasına” (vanishing gradients) neden olabilir çünkü Softmax fonksiyonu “bir-sıcak” (one-hot) vektöre yaklaşır ve türevi neredeyse sıfır olur. Bu nedenle, eğitim sırasında $\beta$’nın dikkatli bir şekilde başlatılması veya ısıtılması (annealing) gerekebilir.25
8. Sonuç ve Gelecek Perspektifi
Modern Hopfield Ağları, yapay zeka tarihinde nadir görülen bir birleşimi temsil eder: Teorik fizik, biyoloji ve modern derin öğrenme mühendisliği bu noktada kesişmiştir. 1980’lerin “unutulmuş” teknolojisi, matematiksel bir modifikasyonla (enerji fonksiyonunun dikleştirilmesi) 2020’lerin en güçlü yapay zeka motoruna (Transformer) dönüşmüştür.
Temel Çıkarımlar:
- Kapasite Sorunu Çözülmüştür: Üstel enerji fonksiyonları sayesinde, bellek kapasitesi artık bir darboğaz değildir.
- Transformer’lar Birer Hopfield Ağıdır: LLM’lerin başarısı, aslında çok büyük ve verimli bir ilişkisel bellek olmalarından kaynaklanmaktadır.
- Güvenlik İçin İdealdir: Yüksek enerjili etkileşimler, adversarial saldırılara karşı doğal bir kalkan oluşturur.
Gelecek Yönelimleri: Araştırmalar şu anda “Energy Transformer” (Et) modellerine odaklanmaktadır.26 Bu modeller, Transformer’ın sadece dikkat kısmını değil, tüm mimarisini (ileri beslemeli katmanlar dahil) tek bir enerji fonksiyonunun minimizasyonu olarak kurgulamayı hedefler. Bu, yapay zekanın “kara kutu” olmaktan çıkıp, şeffaf, kararlı ve yorumlanabilir fiziksel sistemlere dönüşmesinin yolunu açacaktır. NASA için bu, uzayın derinliklerinde kendi kendine karar verebilen, hataya dayanıklı ve açıklanabilir yapay zeka sistemleri anlamına gelmektedir.
Tablo 1: Hopfield Ağı Nesillerinin Karşılaştırmalı Analizi
| Özellik | Klasik Hopfield Ağı (1982) | Yoğun İlişkisel Bellek (DAM) (2016) | Modern Hopfield Ağı (2020) |
| Durum Değişkeni | İkili (Binary) $\{-1, 1\}$ | İkili veya Sürekli | Sürekli (Continuous) $\mathbb{R}^d$ |
| Etkileşim Tipi | İkili ($x_i x_j$) – Karesel | Polinom ($x^n$) – Yüksek Dereceli | Üstel ($e^x$) – Transcendental |
| Depolama Kapasitesi | $\approx 0.14 N$ (Lineer) | $\approx N^{n-1}$ (Süper-Lineer) | $\approx 2^{d/2}$ (Üstel) |
| Hata Toleransı | Düşük (Kapasite aşımında çöküş) | Orta (Polinom derecesine bağlı) | Çok Yüksek (Keskin enerji çukurları) |
| Güncelleme Kuralı | İşaret (Sign) Fonksiyonu | Rektifiye Polinom (ReP) | Softmax (Attention) |
| Yakınsama Hızı | Yavaş (Çoklu iterasyon) | Hızlı | Genellikle Tek Adım |
| Adversarial Dayanıklılık | Tanımsız (Spurious minima sorunu) | Yüksek (Anlamsal prototipler) | Çok Yüksek (Gradientsiz platolar) |
| Derin Öğrenme Karşılığı | RNN (Basit) | ReLU Ağları (Limit durumunda) | Transformer (Self-Attention) |
Rapor Sonu.
Alıntılanan çalışmalar
- Hopfield network – Scholarpedia, erişim tarihi Aralık 16, 2025, http://www.scholarpedia.org/article/Hopfield_network
- New research in Hopfield Networks: A short intro | by Joe El Khoury – GenAI Engineer, erişim tarihi Aralık 16, 2025, https://medium.com/@jelkhoury880/new-research-in-hopfield-networks-a-short-intro-6169a20e91c2
- Hopfield Networks is All You Need – Institute for Machine Learning @ JKU, erişim tarihi Aralık 16, 2025, https://ml-jku.github.io/hopfield-layers/
- On the Role of Hidden States of Modern Hopfield Network in Transformer – arXiv, erişim tarihi Aralık 16, 2025, https://arxiv.org/html/2511.20698v1
- Improved Robustness and Hyperparameter Selection in Modern Hopfield Networks, erişim tarihi Aralık 16, 2025, https://www.researchgate.net/publication/382251202_Improved_Robustness_and_Hyperparameter_Selection_in_Modern_Hopfield_Networks
- Dense Associative Memory Is Robust to Adversarial Inputs – ResearchGate, erişim tarihi Aralık 16, 2025, https://www.researchgate.net/publication/312061182_Dense_Associative_Memory_Is_Robust_to_Adversarial_Inputs
- Hopfield network – Wikipedia, erişim tarihi Aralık 16, 2025, https://en.wikipedia.org/wiki/Hopfield_network
- Robust Exponential Memory in Hopfield Networks – PMC – NIH, erişim tarihi Aralık 16, 2025, https://pmc.ncbi.nlm.nih.gov/articles/PMC5770423/
- [1606.01164] Dense Associative Memory for Pattern Recognition – arXiv, erişim tarihi Aralık 16, 2025, https://arxiv.org/abs/1606.01164
- Dense Associative Memory for Pattern Recognition – NIPS papers, erişim tarihi Aralık 16, 2025, http://papers.neurips.cc/paper/6121-dense-associative-memory-for-pattern-recognition.pdf
- Chapter 3 – Adversarial examples, solving the inner maximization, erişim tarihi Aralık 16, 2025, https://adversarial-ml-tutorial.org/adversarial_examples/
- TOWARDS NATURAL ROBUSTNESS AGAINST ADVERSARIAL EXAMPLES – OpenReview, erişim tarihi Aralık 16, 2025, https://openreview.net/pdf?id=RrSuwzJfMQN
- [1701.00939] Dense Associative Memory is Robust to Adversarial Inputs – arXiv, erişim tarihi Aralık 16, 2025, https://arxiv.org/abs/1701.00939
- [PDF] Hopfield Networks is All You Need – Semantic Scholar, erişim tarihi Aralık 16, 2025, https://www.semanticscholar.org/paper/Hopfield-Networks-is-All-You-Need-Ramsauer-Schafl/804a6d7c23335bbca6eec3b7d3c8366dcbe395a5
- Hopfield Networks is All You Need – OpenReview, erişim tarihi Aralık 16, 2025, https://openreview.net/forum?id=tL89RnzIiCd
- Hopfield Networks is All You Need – OpenReview, erişim tarihi Aralık 16, 2025, https://openreview.net/pdf/4dfbed3a6ececb7282dfef90fd6c03812ae0da7b.pdf
- Universal Hopfield Networks: A General Framework for Single-Shot Associative Memory Models – PMC – NIH, erişim tarihi Aralık 16, 2025, https://pmc.ncbi.nlm.nih.gov/articles/PMC7614148/
- Modern Hopfield Networks and Attention for Immune Repertoire Classification – bioRxiv, erişim tarihi Aralık 16, 2025, https://www.biorxiv.org/content/10.1101/2020.04.12.038158v3.full-text
- (PDF) Modern Hopfield Networks and Attention for Immune Repertoire Classification, erişim tarihi Aralık 16, 2025, https://www.researchgate.net/publication/343253477_Modern_Hopfield_Networks_and_Attention_for_Immune_Repertoire_Classification
- Affinity maturation for an optimal balance between long-term immune coverage and short-term resource constraints – NIH, erişim tarihi Aralık 16, 2025, https://pmc.ncbi.nlm.nih.gov/articles/PMC8872716/
- Affinity maturation for an optimal balance between long-term immune coverage and short-term resource constraints – bioRxiv, erişim tarihi Aralık 16, 2025, https://www.biorxiv.org/content/10.1101/2021.07.26.453765v1.full.pdf
- Latent Structured Hopfield Network for Semantic Association and Retrieval – arXiv, erişim tarihi Aralık 16, 2025, https://arxiv.org/html/2506.01303v2
- The Log-Sum-Exp Trick – Gregory Gundersen, erişim tarihi Aralık 16, 2025, https://gregorygundersen.com/blog/2020/02/09/log-sum-exp/
- Feature request: logsumexp · Issue #2591 · pytorch/pytorch – GitHub, erişim tarihi Aralık 16, 2025, https://github.com/pytorch/pytorch/issues/2591
- A Gentle Introduction to torch.autograd – PyTorch, erişim tarihi Aralık 16, 2025, https://docs.pytorch.org/tutorials/beginner/blitz/autograd_tutorial.html
- Dmitry Krotov | Modern Hopfield Networks for Novel Transformer Architectures – YouTube, erişim tarihi Aralık 16, 2025, https://www.youtube.com/watch?v=5LXiQUsnHrI
Modern Hopfield Networks for Novel Transformer Architectures – Harvard CMSA, erişim tarihi Aralık 16, 2025, https://cmsa.fas.harvard.edu/event/nt-51023/







4 thoughts on “Modern Hopfield Ağları ve Yoğun İlişkisel Bellek Mimarileri”