Büyük Dil Modellerinde Softmax Fonksiyonu

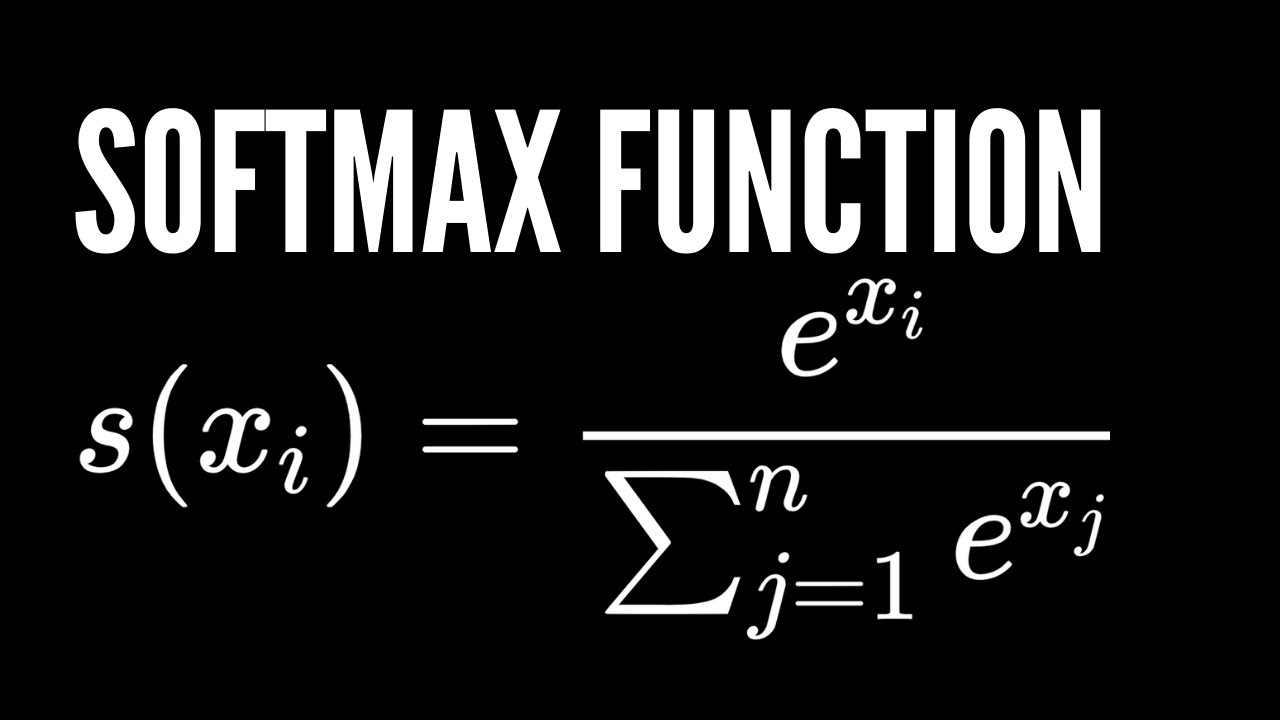
1. Giriş: Softmax Nedir ve Neden İhtiyaç Duyarız?

Büyük Dil Modelleri (LLM’ler), özünde karmaşık matematiksel işlemler yapan devasa hesap makineleridir. Bu makineler, bir sonraki kelimeyi tahmin etmeye çalışırken, işlem sonunda Logit adı verilen ham sayılar üretirler.

Terim Açıklaması: Logit (Log-odds)

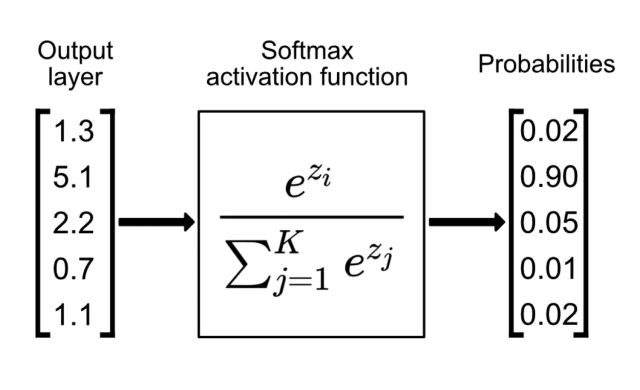
Logit, bir modelin son katmanından çıkan, herhangi bir sınırlaması olmayan (eksi sonsuzdan artı sonsuza gidebilen) ham puanlardır. Örneğin, bir modelin “kedi” için ürettiği logit 5.0, “köpek” için 2.0 olabilir. Bu sayılar tek başlarına bir olasılık ifade etmezler çünkü toplamları 1 değildir ve negatif olabilirler.

Softmax fonksiyonu, bu ham, kuralsız ve yorumlaması zor olan Logit değerlerini, toplamı tam olarak 1.0 (%100) olan ve 0 ile 1 arasında değişen Olasılık değerlerine dönüştüren matematiksel işlemdir. Bu işlem, yapay zekanın “karar verme” mekanizmasıdır. Modelin ürettiği sayısal karmaşayı, “Bu kelimenin gelme ihtimali %80, şununki %20” gibi insan tarafından anlaşılabilir bir formata sokar.

Softmax Büyük Dil Modellerinde Softmax Fonksiyonu: Temel Kavramlardan İleri Mühendisliğe Bilgisayar Bilimleri/Yapay Zeka

Şu yazılar ilginizi çekebilir.

2. Fiziksel ve Matematiksel Kökenler

Softmax, bilgisayar bilimciler tarafından sıfırdan uydurulmuş bir formül değildir. Kökeni, 19. yüzyıl fiziğine, termodinamiğe dayanır.

2.1 Boltzmann Dağılımı ve Termodinamik

Fizikte, parçacıkların enerjileri ile belirli bir durumda bulunma olasılıkları arasındaki ilişkiyi anlamak için bazı sabitlere ve dağılımlara ihtiyaç vardır.

Terim Açıklaması: Boltzmann Sabiti ($k_B$)

Avusturyalı fizikçi Ludwig Boltzmann’ın adını taşıyan bu sabit, sıcaklık ile enerji arasındaki ilişkiyi kuran temel bir fiziksel sabittir. Basitçe, bir parçacığın sahip olduğu ısı enerjisinin, onun hareketine (kinetik enerjisine) nasıl dönüştüğünü gösteren bir katsayıdır.

Terim Açıklaması: Bölüşüm Fonksiyonu (Partition Function – $Z$)

Bir sistemdeki tüm olası durumların toplamını ifade eder. Olasılık hesaplarken “payda” kısmına yazılarak, tekil olasılıkların toplamının 1 olmasını sağlayan normalizasyon katsayısıdır.

Fizikte, bir sistemin $i$ durumunda bulunma olasılığı ($p_i$), o durumun enerjisine ($E_i$) ve sıcaklığa ($T$) bağlıdır:

$$p_i = \frac{e^{-E_i / k_B T}}{Z}$$

Yapay zekada ise Softmax, bu formülün doğrudan uyarlamasıdır. Bizim dünyamızda “Enerji” yerine “Logitler” ($z_i$), fiziksel sıcaklık yerine ise modelin kararlılığını etkileyen “Sıcaklık (Temperature)” parametresi ($\tau$) kullanılır.¹

$$S(z_i) = \frac{e^{z_i / \tau}}{\sum_{j=1}^K e^{z_j / \tau}}$$

Burada:

$e^{z_i}$: Logit değerinin üstel (exponential) karşılığıdır. Logit arttıkça bu değer patlayarak büyür, bu da modelin yüksek puan verdiği seçeneği “kazanan” olarak belirginleştirmesini sağlar.
$\sum e^{z_j}$: Tüm olası logitlerin üstel toplamıdır (Fizikteki $Z$). Paydadaki bu ifade, sonucun 0-1 arasına sıkışmasını garanti eder.

3. Softmax’ın Matematiği: Türevler ve Öğrenme

Yapay zeka modelleri “Geri Yayılım” (Backpropagation) adı verilen bir yöntemle öğrenir. Bu yöntem, modelin hatasını azaltmak için parametreleri ne kadar değiştirmemiz gerektiğini hesaplar. Bu hesaplama için fonksiyonların türevlenebilir olması şarttır.

3.1 Jacobian Matrisi Nedir?

Softmax vektörel bir fonksiyon olduğu için (bir liste sayı girer, bir liste sayı çıkar), türevi tek bir sayı değil, bir matristir.

Terim Açıklaması: Jacobian Matrisi

Jacobian matrisi, çok girdili ve çok çıktılı bir fonksiyonun tüm kısmi türevlerini içeren bir tablodur. Basitçe; “Girdi listesindeki 3. sayıyı çok az değiştirirsem, çıktı listesindeki 1., 2., 3…. ve sonuncu sayılar bundan nasıl etkilenir?” sorusunun cevabını veren tablodur.

Softmax’ta Jacobian matrisine ihtiyaç duymamızın sebebi şudur: Softmax’ın paydasında tüm sayıların toplamı vardır. Dolayısıyla, girdilerden sadece birini ($z_k$) değiştirmek, paydayı değiştireceği için tüm çıktıları ($S_1, S_2,… S_n$) değiştirir. Her şey birbirine bağlıdır.⁴

Jacobian Matrisinin formülü şöyledir:

$$\frac{\partial S_i}{\partial z_j} = S_i (\delta_{ij} – S_j)$$

Burada:

Eğer $i=j$ ise (kendi çıktısına etkisi): $S_i(1 – S_i)$ (Pozitif etki).
Eğer $i \neq j$ ise (başkasının çıktısına etkisi): $-S_i S_j$ (Negatif etki).
Anlamı: Bir sınıfın olasılığını artırırsanız, diğerlerinin olasılığını çalmak (azaltmak) zorundasınız çünkü toplam her zaman 1 olmalıdır.

3.2 Loss Fonksiyonu ve Çapraz Entropi (Cross-Entropy)

Modelin ne kadar “yanlış” yaptığını ölçmemiz gerekir. Bunu ölçen araca Loss (Yitim/Kayıp) Fonksiyonu denir.

Terim Açıklaması: Loss Fonksiyonu

Modelin tahmini ile gerçek sonuç arasındaki farkı (hatayı) hesaplayan formüldür. Amaç, eğitim sırasında bu “Loss” değerini sıfıra yaklaştırmaktır.

Terim Açıklaması: One-Hot Encoding

Gerçek cevabın matematiksel temsilidir. Örneğin hedef “Kedi” ise ve sınıflarımız [Kuş, Kedi, Köpek] ise, one-hot vektörümüz olur.

Softmax genellikle Kategorik Çapraz Entropi (Cross-Entropy) loss fonksiyonu ile birlikte kullanılır. Matematiksel bir “sihir” sonucu, Softmax ve Çapraz Entropi’nin türevleri birbirini sadeleştirir ve geriye çok basit bir ifade kalır:

$$\text{Gradyan (Hata Sinyali)} = S_i – y_i$$

Yani modelin öğrenmek için kullandığı sinyal, sadece (Tahmin Edilen Olasılık – Gerçek Olasılık) farkıdır. Bu basitlik, milyarlarca parametreli modellerin hızlı eğitilmesini sağlayan en önemli faktörlerden biridir.

4. Sayısal Kararlılık: Bilgisayarların Sınırları

Kağıt üzerinde sonsuz büyüklükteki sayılarla işlem yapabiliriz ancak bilgisayarlarda sayıların bir sınırı vardır.

4.1 Overflow (Taşma) Problemi

Softmax formülündeki $e^x$ (üstel fonksiyon) çok hızlı büyür.

$e^{10} \approx 22,000$
$e^{100} \approx 2.6 \times 10^{43}$
$e^{1000} \to$ Bilgisayar hafızasına sığmaz (Overflow Hatası).

Eğer modelin ürettiği logitlerden biri çok büyükse (örneğin 1000), bilgisayar bunu “Sonsuz” ($\infty$) olarak kabul eder. Sonsuz bölü sonsuz belirsizliği oluşur ve program çökerek NaN (Not a Number) hatası verir.

4.2 Log-Sum-Exp Hilesi (Mühendislik Çözümü)

Bu sorunu çözmek için Log-Sum-Exp adı verilen bir numara kullanılır. Matematiksel olarak, Softmax fonksiyonunda tüm girdilerden sabit bir sayı çıkarmak sonucu değiştirmez.

Mühendisler, hesaplama yapmadan önce tüm logitlerden, o vektördeki en büyük sayıyı ($z_{max}$) çıkarırlar.

Böylece en büyük sayı $0$ olur ($e^0 = 1$).
Diğer tüm sayılar negatif olur ($e^{-5}$, $e^{-20}$ gibi).
Negatif sayıların üsteli 0 ile 1 arasındadır.
Sonuç: Asla patlama (overflow) olmaz. İşlem matematiksel olarak tamamen aynıdır ama bilgisayar için güvenlidir.

5. LLM ve Transformer Mimarisindeki Yeri

Softmax, modern yapay zekanın (GPT, Llama, Gemini) belkemiği olan Transformer mimarisinde iki kritik noktada kullanılır.

5.1 Dikkat Mekanizması (Attention Mechanism)

Transformer’ların kelimeler arasındaki ilişkiyi anlamasını sağlayan Self-Attention (Öz-Dikkat) mekanizmasında Softmax, bir “odaklanma filtresi” görevi görür.

Formül:

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$$

Burada Softmax, modelin o anki kelime için geçmişteki hangi kelimelere ne kadar dikkat etmesi gerektiğini belirleyen 0 ile 1 arasındaki ağırlıkları üretir.

Neden $\sqrt{d_k}$’ye bölüyoruz?

Logitler (burada $QK^T$) çok büyürse, Softmax fonksiyonu uç noktalara (0 veya 1’e) çok yaklaşır. Bu noktalarda fonksiyonun eğimi (türevi) neredeyse sıfırdır. Türev sıfır olursa model öğrenemez (Gradient Vanishing). Sayıları küçültmek ($\sqrt{d_k}$ ile bölmek), Softmax’ın türevlenebilir, verimli bölgesinde kalmasını sağlar.

5.2 Dikkat Çukurları (Attention Sinks) – “Sum-to-One” Sorunu

Softmax’ın “Çıktıların toplamı mutlaka 1 olmalıdır” kuralı, LLM’lerde ilginç bir yan etkiye sebep olur: Attention Sink (Dikkat Çukuru).

Eğer model o an, geçmişteki kelimelerin hiçbirini önemli bulmuyorsa (dikkat edilecek bir şey yoksa), Softmax yine de elindeki %100’lük dikkat puanını bir yerlere dağıtmak zorundadır (çünkü toplam 1 olmak zorunda). Model, bu “fazla” puanı genellikle cümlenin en başındaki anlamsız tokenlara (örneğin cümle başı sembolüne) yığar. Bu tokenlar, gereksiz dikkat puanlarını emen bir “çöp kutusu” (sink) görevi görür.

6. Kod Çözme (Decoding) ve Yaratıcılık Ayarları

Model eğitimi bittikten sonra metin üretirken, Softmax’ın ürettiği olasılıkları nasıl kullandığımız, modelin “karakterini” belirler.

6.1 Sıcaklık (Temperature)

Softmax formülündeki $\tau$ parametresidir.

Düşük Sıcaklık ($\tau < 1$): Olasılık farklarını abartır. %60 olan ihtimali %99 yapar. Model çok tutarlı, ezberci ve robotik olur.
Yüksek Sıcaklık ($\tau > 1$): Olasılık farklarını törpüler, dağılımı düzleştirir. Nadir kelimelerin şansı artar. Model daha “yaratıcı” ve rastgele olur, ancak saçmalama (halüsinasyon) riski artar.⁶

6.2 Top-k ve Nucleus (Top-p) Örnekleme

Softmax tüm kelime hazinesi (örneğin 100.000 kelime) için olasılık üretir. Ancak “Zebra” kelimesinden sonra “uçtu” gelme ihtimali 0.00001 olsa da vardır. Rastgele seçimde bu gelmesin diye filtreler kullanılır:

Top-k: Sadece en yüksek puanlı k (örn. 50) kelimeyi dikkate al, gerisini çöpe at.
Top-p (Nucleus): Toplam olasılık değeri %p (örn. %90) olana kadar en yüksekten başlayarak kelimeleri seç. Bu yöntem, modelin emin olduğu durumlarda az, kararsız olduğu durumlarda çok seçenek sunarak daha doğal bir dil üretimi sağlar.

7. Güncel Gelişmeler ve Softmax’ın Ötesi (2024-2025)

Teknoloji geliştikçe Softmax’ın bazı sınırları zorlanmaktadır.

7.1 “Massive Activations” ve Kuantizasyon Sorunu

Softmax, yapısı gereği “kazanan hepsini alır” mantığına yakındır. Bu durum, modelin içindeki bazı nöronların çok devasa değerler (outlier) üretmesine neden olur. Bu devasa değerler, modelleri küçültmeyi (Quantization: 16-bit’ten 4-bit’e düşürme) zorlaştırır. Çünkü 4-bitlik küçük bir alana bu devasa sayıları sığdırmaya çalışmak, diğer hassas bilgilerin kaybolmasına yol açar.

7.2 DeepSeek V3 ve Sigmoid Dikkat (Sigmoid Attention)

Yeni nesil modellerden DeepSeek V3, bazı mekanizmalarında Softmax yerine Sigmoid fonksiyonuna geçiş yapmıştır.

Softmax: Seçenekler birbiriyle yarışır (Toplam 1 olmak zorunda). Biri artarsa diğeri azalır.
Sigmoid: Her seçenek bağımsızdır (Her biri 0 ile 1 arasında olabilir).

DeepSeek V3, “Uzmanların Karışımı” (Mixture of Experts – MoE) mimarisinde, hangi uzmanın kullanılacağına karar verirken Sigmoid kullanır. Böylece model, “Bu soru için hem Matematik uzmanına hem de Fizik uzmanına ihtiyacım var” diyebilir ve ikisine de yüksek puan verebilir. Softmax kullansaydı, puanı bölüştürmek zorunda kalırdı ve uzmanların etkisi azalırdı.⁷

8. Sonuç

Softmax, sadece basit bir matematik formülü değil; istatistiksel fizik, bilgi teorisi ve modern bilgisayar mimarisinin kesişim noktasıdır. “Logit”leri “Olasılık”lara çevirerek, makinelerin belirsiz bir dünyada karar vermesini sağlar. Her ne kadar “Toplam 1 olma zorunluluğu” gibi kısıtlamaları Attention Sink gibi yan etkilere yol açsa da, türevlenebilir yapısı ve kararlılığı sayesinde LLM’lerin en temel yapı taşı olmaya devam etmektedir.