Büyük Dil Modellerinde (LLM) Doğrultulmuş Doğrusal Birimler

1. Giriş: Yapay Zekanın Doğrusal Olmayan Kalbi

Bilgisayar bilimlerinin en hızlı gelişen alt disiplini olan yapay zeka ve özellikle Derin Öğrenme (Deep Learning), temelinde insan beyninin bilgi işleme mekanizmalarını taklit etmeye çalışan, ancak matematiksel aksiyomlar üzerine kurulu karmaşık sistemlerdir. Günümüzde “Yapay Zeka” olarak adlandırdığımız Büyük Dil Modelleri (Large Language Models – LLM’ler), milyarlarca parametre içeren devasa matematiksel fonksiyonlardan ibarettir. Bu fonksiyonların karmaşık, çok boyutlu veri uzaylarını (örneğin, insan dilinin tüm anlamsal yapısını) modelleyebilmesinin arkasındaki temel güç, mimarinin derinliği veya parametre sayısından ziyade, “aktivasyon fonksiyonu” (activation function) adı verilen basit ama hayati bir bileşenden kaynaklanmaktadır.¹

Bu rapor, modern yapay sinir ağlarının en ikonik ve dönüştürücü bileşenlerinden biri olan Doğrultulmuş Doğrusal Birim (Rectified Linear Unit – ReLU) kavramını, bir bilgisayar bilimi profesörü perspektifiyle, en ince nüanslarına kadar incelemeyi amaçlamaktadır. ReLU, yapay sinir ağlarının “sığ” ve eğitilmesi zor yapılardan, bugün bildiğimiz “derin” ve insan seviyesinde performans gösteren mimarilere dönüşmesini sağlayan kritik bir kaldıraçtır.³ Ancak bu hikaye sadece geçmişle sınırlı değildir; Llama, GPT ve PaLM gibi modern mimarilerde ReLU’nun rolü, daha karmaşık varyasyonları (GELU, SwiGLU) ve son dönemde verimlilik odaklı geri dönüşü (Sparsity/Seyreklik) ile sürekli evrilmektedir.

Bu analizde, öncelikle yapay sinir ağlarının temel yapı taşları olan ağırlıklar (weights) ve sapmalar (biases) tanımlanacak, ardından doğrusallık (linearity) ve doğrusal olmama (non-linearity) kavramlarının teorik zorunluluğu tartışılacaktır. Akabinde, ReLU’nun matematiksel anatomisi, eğitim dinamikleri üzerindeki etkisi, “Ölü ReLU” (Dying ReLU) gibi patolojileri ve modern Transformer mimarilerindeki yerini alan gelişmiş varyantları detaylandırılacaktır.

Şu yazılar ilginizi çekebilir.

2. Nöral Hesaplamanın Temel Bileşenleri

ReLU’nun işlevini tam olarak kavrayabilmek için, bir yapay nöronun (artificial neuron) aktivasyon fonksiyonundan hemen önce gerçekleştirdiği işlemleri atomlarına ayırmak gerekir. Derin öğrenme literatüründe sıkça karşılaşılan “ağırlık” ve “sapma” terimleri, soyut kavramlar değil, lineer cebirin somut operatörleridir.

2.1 Ağırlıklar (Weights): Sinyal Şiddetinin Belirleyicisi

Bir yapay sinir ağında ağırlıklar, iki nöron arasındaki bağlantının gücünü ve yönünü temsil eden öğrenilebilir parametrelerdir.⁵ Biyolojik bir benzetme yapılacak olursa, ağırlıklar sinapsların iletkenlik kapasitesine karşılık gelir. Matematiksel olarak ağırlıklar, giriş verisi ile çarpılan skaler değerlerdir ($w \cdot x$).

Bir Büyük Dil Modeli (LLM) bağlamında düşünüldüğünde, ağırlıklar modelin “bilgisini” saklayan depolardır. Eğitim süreci boyunca, model milyonlarca metin örneği üzerinden geçerken, bu ağırlık değerleri iteratif olarak güncellenir. Ağırlığın büyüklüğü, giriş sinyalinin (input) çıkış (output) üzerindeki etkisinin ne kadar baskın olacağını belirler.⁶

Pozitif Ağırlık: Giriş sinyali arttıkça, nöronun aktivasyon potansiyelini artırır (uyarıcı etki).
Negatif Ağırlık: Giriş sinyali arttıkça, nöronun aktivasyon potansiyelini baskılar (inhibe edici etki).
Sıfıra Yakın Ağırlık: Giriş sinyalinin nöron üzerinde neredeyse hiç etkisi yoktur; bağlantı önemsizdir.

Bu çarpma işlemi ($input \times weight$), sinir ağının verideki örüntüleri tanıması için kullandığı temel mekanizmadır.

2.2 Sapmalar (Biases): Aktivasyon Eşiği

Sapmalar veya literatürdeki adıyla “bias”lar, bir nörona eklenen ve herhangi bir girişten bağımsız olan sabit değerlerdir. Ağırlıklar giriş verisiyle çarpılırken, sapmalar bu çarpıma toplanarak eklenir ($wx + b$).

Sapmanın temel görevi, aktivasyon fonksiyonunu koordinat düzleminde kaydırmaktır.⁶ Bir nöronun sadece ağırlıklara sahip olduğunu düşünelim; eğer tüm girişler ($x$) sıfır ise, ağırlıklarla çarpımın sonucu daima sıfır olacaktır. Bu durum, modelin esnekliğini ciddi şekilde kısıtlar. Sapma parametresi, girişler sıfır olsa bile nöronun belirli bir baz değer üretmesini sağlar.

Daha sezgisel bir açıklama ile sapma, nöronun ne kadar kolay “ateşleneceğini” (aktive olacağını) belirleyen bir eşik değeridir.⁸

Yüksek Pozitif Sapma: Nöron, düşük giriş sinyallerinde bile aktif olmaya meyillidir.
Yüksek Negatif Sapma: Nöronun aktif olabilmesi için çok güçlü bir giriş sinyaline ihtiyacı vardır (eşik yükselmiştir).

Sonuç olarak, bir nöronun aktivasyon fonksiyonuna girmeden önceki hali, lineer bir afin dönüşümdür:

$$z = \sum (w_i \cdot x_i) + b$$

Burada $z$, “pre-aktivasyon” değeri olarak adlandırılır.

2.3 Doğrusallık Sorunu ve Aktivasyon Fonksiyonunun Gerekliliği

Eğer yapay sinir ağları sadece ağırlıklar ve sapmalardan oluşsaydı, ne kadar derin (katmanlı) olurlarsa olsunlar, karmaşık problemleri çözemezlerdi. Bu, lineer cebirin temel bir kuralından kaynaklanır: İki doğrusal fonksiyonun bileşkesi, yine doğrusal bir fonksiyondur.²

Matematiksel olarak kanıtlamak gerekirse:

Birinci katman fonksiyonu $f(x) = W_1x + b_1$ olsun.

İkinci katman fonksiyonu $g(y) = W_2y + b_2$ olsun.

Bu iki katmanı ardışık bağladığımızda (derin ağ):

$$g(f(x)) = W_2(W_1x + b_1) + b_2 = (W_2W_1)x + (W_2b_1 + b_2)$$

Bu denklemde $W_2W_1$ yeni bir matris ($W’$), $W_2b_1 + b_2$ ise yeni bir vektör ($b’$) olarak ifade edilebilir. Sonuçta elde edilen yapı, tek katmanlı bir lineer dönüşüme ($W’x + b’$) eşdeğerdir.

Bu durum, “katmanların çökmesi” (layer collapse) olarak bilinir. Aktivasyon fonksiyonu olmadan, milyarlarca parametreli bir GPT modelinin hesaplama gücü, basit bir lineer regresyon modeline indirgenir.⁹ Ancak gerçek dünya verileri (insan dili, görseller, ses dalgaları) doğrusal değildir (non-linear). Kelimeler arasındaki ilişkiler, piksellerin oluşturduğu şekiller veya finansal verilerdeki trendler, düz çizgilerle ifade edilemez.

İşte bu noktada Aktivasyon Fonksiyonu devreye girer. Aktivasyon fonksiyonu, nöronun lineer çıktısına ($z$) uygulanan ve doğrusal olmayan bir matematiksel işlemdir ($a = \sigma(z)$). Bu işlem, ağın düz çizgileri bükmesini, eğip bükmesini ve karmaşık karar sınırları oluşturmasını sağlar.¹

Evrensel Yaklaşıklık Teoremi (Universal Approximation Theorem), doğrusal olmayan bir aktivasyon fonksiyonuna sahip, yeterli sayıda nöron içeren tek bir gizli katmanlı ağın bile, teorik olarak her türlü sürekli fonksiyonu modelleyebileceğini belirtir.² Dolayısıyla, aktivasyon fonksiyonu, yapay zekanın “öğrenme” kapasitesinin matematiksel anahtarıdır.

3. Doğrultulmuş Doğrusal Birim (ReLU): Tanım ve Teorik Analiz

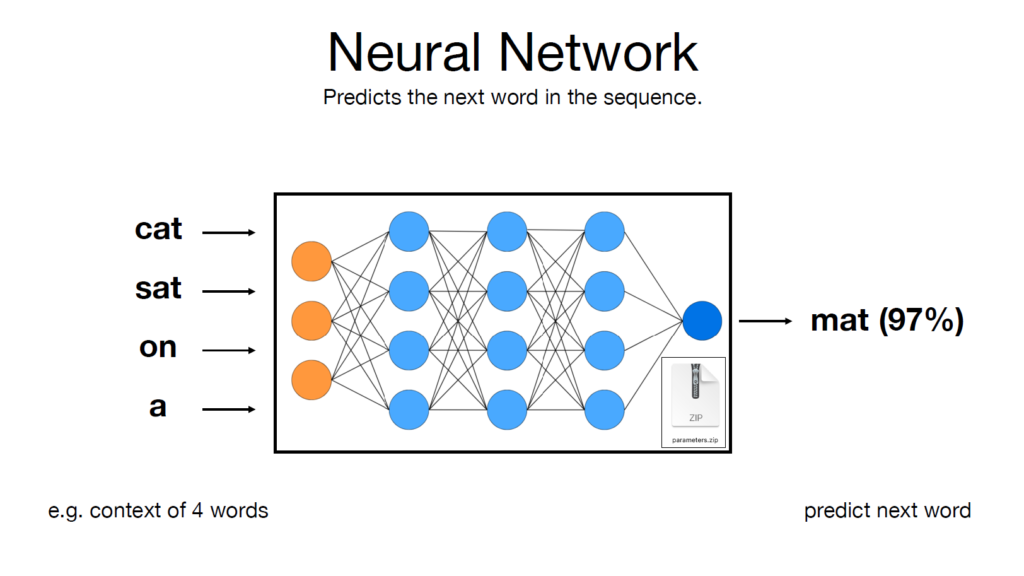
image-2-1024x576 (ReLU) Büyük Dil Modellerinde (LLM) Doğrultulmuş Doğrusal Birimler Bilgisayar Bilimleri/Yapay Zeka

Aktivasyon fonksiyonlarının tarihçesinde, uzun yıllar boyunca Sigmoid ve Hiperbolik Tanjant (Tanh) fonksiyonları hakimiyet sürmüştür. Bu fonksiyonlar, biyolojik nöronların “doygunluk” (saturation) davranışını taklit ettikleri için tercih edilmişlerdir. Ancak 2010’lu yılların başında, derin öğrenme devrimini tetikleyen basit ama güçlü bir fonksiyon sahneye çıkmıştır: ReLU (Rectified Linear Unit).³

3.1 Matematiksel Tanım ve Mekanizma

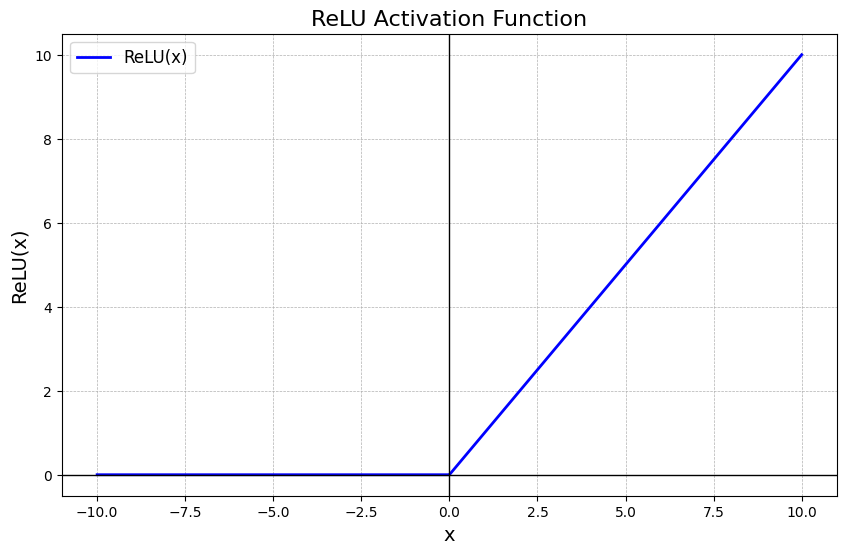
ReLU, son derece basit bir parçalı (piecewise) fonksiyondur. Temel prensibi şudur: Eğer giriş değeri pozitif ise olduğu gibi geçirir, negatif ise tamamen sıfırlar.¹³

Matematiksel formülü:

$$f(x) = \max(0, x)$$

Parçalı fonksiyon gösterimi ile:

$$f(x) = \begin{cases} x & \text{eğer } x > 0 \\ 0 & \text{eğer } x \le 0 \end{cases}$$

“Doğrultulmuş” (Rectified) Teriminin Kökeni:

Bu terim elektrik mühendisliğinden ödünç alınmıştır. Alternatif akımı (AC) doğru akıma (DC) dönüştüren diyotlar, akımın negatif kısmını keserek sadece pozitif kısmın geçmesine izin verir. Bu işleme “doğrultma” (rectification) denir. ReLU nöronu da benzer şekilde, negatif sinyalleri “kesip atarak” (clipping), sadece pozitif aktivasyonları iletir.4

3.2 ReLU’nun Türevi ve Gradyan Akışı

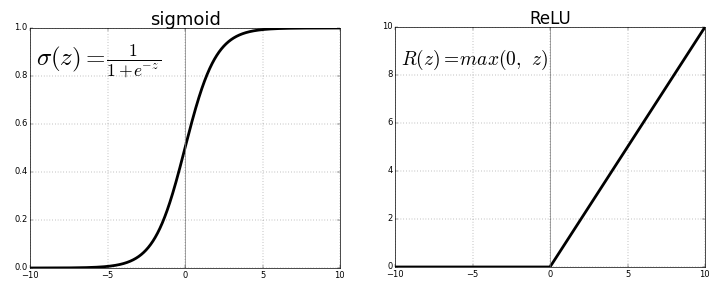
image-3 (ReLU) Büyük Dil Modellerinde (LLM) Doğrultulmuş Doğrusal Birimler Bilgisayar Bilimleri/Yapay Zeka

Derin öğrenme modelleri, Geri Yayılım (Backpropagation) algoritması ile eğitilir. Bu algoritma, hatayı (loss) minimize etmek için ağırlıkların nasıl güncelleneceğini belirleyen türevleri (gradyanları) hesaplar.¹⁴ Dolayısıyla bir aktivasyon fonksiyonunun türevi, fonksiyonun kendisi kadar önemlidir.

ReLU’nun türevi ($f'(x)$) şöyledir:

$$f'(x) = \begin{cases} 1 & \text{eğer } x > 0 \\ 0 & \text{eğer } x < 0 \end{cases}$$

Önemli Nüans: $x=0$ noktasında fonksiyon sürekli olmasına rağmen türevli değildir (soldan türev 0, sağdan türev 1’dir). Ancak pratikte, bilgisayar bilimciler ve yazılım kütüphaneleri (PyTorch, TensorFlow) $x=0$ noktasındaki türevi keyfi olarak 0 veya 0.5 kabul ederek bu matematiksel süreksizliği aşarlar.¹⁶

Bu türev yapısı—yani çıktının ya tam 1 ya da tam 0 olması—ReLU’yu önceki nesil aktivasyon fonksiyonlarından (Sigmoid, Tanh) ayıran en devrimsel özelliktir. Sigmoid fonksiyonunun türevi sürekli değişen ve maksimum 0.25 olan ondalıklı sayılardır. ReLU’da ise nöron aktifse ($x>0$), türev 1’dir ve gradyan bozulmadan akar.

3.3 Manifold Hipotezi ve Topolojik Bakış Açısı

image-4 (ReLU) Büyük Dil Modellerinde (LLM) Doğrultulmuş Doğrusal Birimler Bilgisayar Bilimleri/Yapay Zeka

ReLU’nun neden bu kadar etkili olduğunu anlamak için Manifold Hipotezi‘ne değinmek gerekir. Bu hipotez, yüksek boyutlu verilerin (örneğin 1024 boyutlu bir kelime vektörü), aslında bu yüksek boyutlu uzay içinde gömülü olan çok daha düşük boyutlu bir yapının (manifoldun) üzerinde bulunduğunu savunur.¹⁸

Örneğin, buruşturulmuş bir kağıt topunu düşünün. Kağıt 3 boyutlu uzaydadır, ancak yüzeyi aslında 2 boyutludur. Sinir ağının görevi, bu “buruşturulmuş” veri uzayını açarak, sınıfları (örneğin ‘kedi’ ve ‘köpek’ resimlerini) birbirinden ayıran düz bir çizgi çekebilmektir.

ReLU, bu “açma” işlemini parçalı doğrusal dönüşümlerle yapar. Her ReLU nöronu, uzayı ikiye bölen bir düzlem (hiper-düzlem) yaratır: Bir taraf aktif (lineer bölge), diğer taraf pasif (sıfır bölgesi). Derin bir ağda trilyonlarca ReLU nöronu bir araya geldiğinde, bu basit düzlemler birleşerek verinin karmaşık manifoldunu (o buruşturulmuş kağıdı) poligonlar halinde modeller ve düzleştirir.¹⁸ Bu, ReLU’nun doğrusal olmayan gücünün geometrik yorumudur.

4. Derin Ağlarda Eğitim Dinamikleri ve Kaybolan Gradyan Sorunu

Büyük Dil Modelleri (LLM), doğaları gereği çok derin (çok katmanlı) yapılardır. Örneğin GPT-3, 96 ardışık Transformer katmanından oluşur. Bu derinlik, eğitimin önündeki en büyük engeli, Kaybolan Gradyan Problemini (Vanishing Gradient Problem) doğurur.

4.1 Kaybolan Gradyan Problemi (The Vanishing Gradient Problem)

Geri yayılım sırasında gradyanlar, çıktı katmanından giriş katmanına doğru “zincir kuralı” (chain rule) ile çarpılarak taşınır.

Zincir kuralı:

$$\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial h_n} \cdot… \cdot \frac{\partial h_2}{\partial h_1} \cdot \frac{\partial h_1}{\partial w_1}$$

Eğer Sigmoid fonksiyonu kullanılırsa, türev değeri ($0$ ile $0.25$ arasında) daima 1’den küçüktür.21 Onlarca katman boyunca bu küçük sayıların birbiriyle çarpıldığını düşünün:

$$0.25 \times 0.25 \times 0.25 \times… \approx 0.0000001$$

Sonuç olarak, ağın ilk katmanlarına ulaşan gradyan sinyali o kadar küçülür ki, bilgisayarın hassasiyet sınırlarının altına düşer. İlk katmanlardaki ağırlıklar güncellenemez hale gelir ve ağ öğrenmeyi durdurur. Bu, derin ağların Sigmoid ile eğitilememesinin temel nedenidir.14

4.2 ReLU’nun Çözümü: Gradyan Korunumu

ReLU, bu soruna radikal bir çözüm getirir. Pozitif bölgede ($x>0$) ReLU’nun türevi tam olarak 1’dir.

$$1 \times 1 \times 1 \times… = 1$$

Bir ReLU nöronu aktif olduğu sürece, gradyan sinyalini zayıflatmadan bir önceki katmana aktarır.12 Bu özellik, gradyanların ağın en derin noktalarından en sığ noktalarına kadar “bir otoyol gibi” akmasını sağlar. Bugün 100+ katmanlı LLM’leri eğitebilmemizin arkasındaki temel matematiksel gerçek budur.21

4.3 Hesaplama Verimliliği (Computational Efficiency)

Teorik avantajlarının yanı sıra, ReLU’nun donanım düzeyinde de büyük bir avantajı vardır.

Sigmoid/Tanh: Üstel fonksiyon ($e^x$), bölme ve trigonometrik işlemler gerektirir. Bunlar işlemci (CPU/GPU) döngüleri açısından “pahalı” işlemlerdir.
ReLU: Sadece bir karşılaştırma işlemidir (if x > 0 return x else 0) veya bir max operasyonudur. Bu, donanım seviyesinde tek bir saat döngüsünde (clock cycle) gerçekleştirilebilen çok ucuz bir işlemdir.¹³

Milyarlarca parametreli ve trilyonlarca işlemli modellerde, bu basitlik kümülatif olarak devasa bir enerji ve zaman tasarrufu sağlar.²⁶

5. ReLU’nun Patolojileri: “Ölü ReLU” (Dying ReLU) Problemi

Her ne kadar ReLU, derin öğrenmeyi mümkün kılmış olsa da, kusursuz değildir. En bilinen ve ciddi yan etkisi Ölü ReLU problemidir.²⁸

5.1 Sorunun Mekanizması

Bir ReLU nöronu, eğer negatif bir girdi alırsa 0 çıktısı verir. Daha da önemlisi, bu bölgedeki türevi de 0’dır. Eğer bir nöron, eğitim sırasında ağırlıkları öyle bir güncellenirse ki, eğitim setindeki tüm veriler için negatif girdi ($wx+b < 0$) üretmeye başlarsa, bu nöron bir kısır döngüye girer.

Nöron tüm veriler için 0 çıktısı verir.
Geri yayılım sırasında gelen gradyan 0 ile çarpılır (çünkü yerel türev 0’dır).
Ağırlıklar güncellenemez (çünkü güncelleme miktarı = gradyan $\times$ öğrenme oranı = 0).
Ağırlıklar değişmediği için nöron hep negatif bölgede kalır.

Bu duruma nöronun “ölmesi” denir. Ölü bir nöron, ağın geri kalanı için hiçbir işlev görmez; sadece yer kaplayan, işlevsiz bir matematiksel yüktür. Büyük ağlarda, bazen nöronların %40’a varan kısmı eğitim sırasında ölebilir.³⁰

5.2 Tetikleyiciler

Yüksek Öğrenme Oranı (Learning Rate): Ağırlık güncelleme adımı çok büyük olursa, ağırlıklar aniden nöronu tamamen negatif bölgeye itecek bir değere sıçrayabilir. Buna “gradients knocking neurons off the manifold” (gradyanların nöronları manifold dışına itmesi) denir.²⁴
Kötü Başlangıç Değerleri (Initialization): Eğer sapma (bias) değerleri başlangıçta çok büyük negatif sayılar olarak atanırsa, nöronlar “ölü doğar”.²⁹

5.3 Varyantlar: Leaky ReLU ve Ötesi

Bu sorunu çözmek için Leaky ReLU (Sızıntılı ReLU) geliştirilmiştir. Negatif bölgede 0 yerine çok küçük bir eğim (örneğin $0.01x$) kullanır.

$$f(x) = \max(0.01x, x)$$

Bu sayede, nöron negatif bölgeye düşse bile türev 0.01 olacağı için hala küçük bir gradyan akışı olur ve nöron zamanla “iyileşip” tekrar aktif bölgeye geçebilir.13

Ancak ilginç bir şekilde, Büyük Dil Modelleri (LLM) evriminde Leaky ReLU ana akım olamamıştır. Bunun yerine Transformer mimarileri, daha farklı bir yola, GELU ve SwiGLU gibi “pürüzsüz” (smooth) aktivasyonlara yönelmiştir.

6. Büyük Dil Modellerinde (LLM) Evrim: ReLU’dan GELU ve SwiGLU’ya Geçiş

Transformer mimarisinin ilk tanıtıldığı 2017 tarihli “Attention Is All You Need” makalesinde ReLU kullanılmıştır. Ancak BERT (2018), GPT-2 (2019) ve sonrasındaki Llama, PaLM gibi modellerde saf ReLU terk edilmiştir.

6.1 GELU: Gauss Hatası Doğrusal Birimi (Gaussian Error Linear Unit)

Modern LLM’lerin (GPT serisi, BERT) büyük çoğunluğu GELU aktivasyon fonksiyonunu kullanır. GELU, ReLU’nun deterministik (kesin) yapısını olasılıksal (probabilistic) bir yaklaşımla yumuşatır.³²

Matematiksel Tanım:

GELU, girdiyi ($x$), standart normal dağılımın kümülatif dağılım fonksiyonu (CDF) ile ağırlıklandırır:

$$GELU(x) = x \cdot \Phi(x)$$

Burada $\Phi(x)$, bir Gauss dağılımında (çan eğrisi) rastgele bir değerin $x$’ten küçük olma olasılığıdır.

$x$ çok büyükse $\Phi(x) \approx 1$, dolayısıyla $GELU(x) \approx x$ (ReLU gibi).
$x$ çok küçükse $\Phi(x) \approx 0$, dolayısıyla $GELU(x) \approx 0$ (ReLU gibi).
Fark: $x=0$ civarında keskin bir köşe yerine, yumuşak bir kavis vardır.

Neden GELU?

Pürüzsüzlük (Smoothness): ReLU, 0 noktasında türevsizdir (kırılma noktası). Çok derin ağlarda bu kırılma noktası, optimizasyon yüzeyinde zorluklar çıkarabilir. GELU her noktada türevlenebilir (kavisli) olduğu için gradyan inişinin daha “akıcı” olmasını sağlar.³²
Olasılıksal Yorum: Modern derin öğrenmede “Dropout” gibi teknikler, nöronların rastgele kapanmasını içerir. GELU, bu stokastik (rastgele) süreci aktivasyon fonksiyonunun içine gömer. Girdinin büyüklüğüne göre “kapanma olasılığını” modeller.³³

6.2 SwiGLU: Kapılı Doğrusal Birimler (Gated Linear Units)

En güncel modellerde (Google’ın PaLM, Meta’nın Llama 2 ve Llama 3 modelleri), SwiGLU adı verilen daha karmaşık bir yapı standart hale gelmiştir.³⁵

GLU (Gated Linear Unit) Mekanizması:

Kapılı birimler, bilginin akışını kontrol etmek için ikinci bir sinyal kullanır.

$$GLU(x) = (xW) \odot \sigma(xV)$$

Burada $xW$ ana sinyaldir, $xV$ ise bir “kapı” (gate) sinyalidir. $\sigma$ (sigmoid) fonksiyonu 0 ile 1 arasında değer üretir.

Eğer kapı değeri 1’e yakınsa, sinyal geçer.
Eğer kapı değeri 0’a yakınsa, sinyal bloke edilir.
Bu mekanizma, LSTM (Long Short-Term Memory) ağlarından ilham almıştır ve ağın hangi bilginin önemli olduğunu dinamik olarak seçmesine olanak tanır.37

SwiGLU:

SwiGLU, kapı fonksiyonu olarak Sigmoid yerine Swish ($x \cdot \sigma(x)$) fonksiyonunu kullanır.

Noam Shazeer (2020) tarafından yapılan araştırmalar, SwiGLU’nun Transformer modellerinde ReLU ve GELU’ya göre daha iyi performans (daha düşük perplexity) sağladığını kanıtlamıştır.39 Bu nedenle Llama gibi modern modeller, hesaplama maliyeti biraz daha yüksek olsa da (iki matris çarpımı gerektirir), öğrenme verimliliği (sample efficiency) daha yüksek olduğu için SwiGLU kullanmaktadır.

7. Seyreklik (Sparsity) ve ReLU’nun Geri Dönüşü: “ReLU Strikes Back”

Yapay zeka dünyasında tarih tekerrür etmektedir. Son iki yılda (2023-2024), GELU ve SwiGLU’nun hakimiyetine rağmen, araştırmacılar tekrar eski dostları ReLU’ya dönmeye başlamıştır. Bu akıma literatürde “ReLU Strikes Back” (ReLU’nun Geri Dönüşü) adı verilmektedir.⁴²

7.1 Pürüzsüzlüğün Maliyeti

GELU ve SwiGLU’nun en büyük dezavantajı, Sparsity (Seyreklik) özelliğini yok etmeleridir.

ReLU: Negatif girdiler için tam olarak 0 çıktısı verir. Bir ReLU ağında, nöronların %50-%90’ı herhangi bir anda tam olarak 0 değerindedir.⁴⁴
GELU/Swish: Negatif girdiler için çok küçük ama sıfırdan farklı sayılar (örneğin -0.0001) üretir. Bilgisayar hafızasında 0 ile 0.0001 aynı yer kaplar (32-bit veya 16-bit).

7.2 Çıkarım (Inference) Darboğazı ve Donanım Gerçekleri

Günümüzde LLM’leri eğitmekten ziyade çalıştırmak (inference/çıkarım) büyük bir maliyet kalemidir. Modern GPU’larda (NVIDIA H100 gibi), işlem gücü (FLOPS) o kadar yüksektir ki, darboğaz artık işlem yapma hızı değil, bellekten veri taşıma hızıdır (Memory Bandwidth Bottleneck).

İşte ReLU’nun “Süper Gücü” burada devreye girer: Seyreklik.

Eğer bir nöronun çıktısı tam olarak 0 ise:

Bu değeri bellekte saklamaya veya okumaya gerek yoktur (Sparse Matrix formatları).
Bu değerle yapılacak çarpma işleminin sonucu da 0 olacağı için, işlemciye bu işlemi yaptırmaya gerek yoktur.

Apple ve diğer araştırma grupları tarafından yayınlanan makaleler, modern LLM’lerde aktivasyon fonksiyonu olarak tekrar ReLU kullanıldığında, modelin kalitesinden ödün vermeden 2-3 kat daha hızlı çıkarım yapılabileceğini göstermiştir.⁴² Bu yöntemle, ağın %90’ından fazlasının “sıfır” olduğu durumlarda, donanım sadece “dolu” olan %10’luk kısmı işleyerek büyük bir hız ve enerji tasarrufu sağlar.

7.3 Biyolojik Plazibilite (Biyolojik Gerçekçilik)

Bu geri dönüş, aynı zamanda biyolojik beyin modelleriyle de örtüşmektedir. İnsan beyni, enerji verimliliği açısından son derece seyrek (sparse) çalışır. Nöronlarımızın sadece küçük bir kısmı aynı anda ateşlenir.⁴⁶ ReLU’nun zorladığı seyreklik, beynin enerji koruma stratejisine, sürekli aktif olan GELU/Swish fonksiyonlarından daha yakındır.

8. Karşılaştırmalı Analiz Tablosu

Aşağıdaki tablo, Büyük Dil Modellerinde kullanılan temel aktivasyon fonksiyonlarının yapısal ve işlevsel farklarını özetlemektedir:

Özellik	ReLU (Rectified Linear Unit)	GELU (Gaussian Error Linear Unit)	SwiGLU (Swish-Gated Linear Unit)
Formül	$f(x) = \max(0, x)$	$x \cdot \Phi(x)$	$(xW) \cdot \text{Swish}(xV)$
Türev ($x=0$)	Tanımsız (Pratikte 0 veya 1)	Pürüzsüz (0.5)	Pürüzsüz
Negatif Çıktı	Tam olarak 0	Sıfıra yakın (Negatif olabilir)	Sıfıra yakın
Seyreklik (Sparsity)	Çok Yüksek (%50-%90)	Yok (Yoğun Aktivasyon)	Düşük
Hesaplama Maliyeti	Çok Düşük (Bit işlemi)	Orta (Hata fonksiyonu approx.)	Yüksek (Ekstra matris çarpımı)
Kullanıldığı Modeller	Orijinal Transformer, ResNet	BERT, GPT-2, GPT-3	Llama, Llama 2, Llama 3, PaLM
Avantajı	Çıkarım hızı, Bellek verimliliği	Eğitim kararlılığı, Pürüzsüzlük	Yüksek ifade gücü, Performans

9. Sonuç ve Gelecek Perspektifi

Doğrultulmuş Doğrusal Birim (ReLU), bilgisayar bilimleri tarihinin en basit ama en etkili buluşlarından biridir. $max(0, x)$ gibi ilkokul seviyesinde bir matematiksel işlem, insanlığın ürettiği en karmaşık yapay zeka sistemlerinin temelini oluşturmuştur.

Raporumuzda incelediğimiz üzere, ReLU’nun hikayesi doğrusal olmayan bir evrim izlemektedir:

Yükseliş: Kaybolan Gradyan problemini çözerek Derin Öğrenme devrimini başlattı.
Duraklama: Transformer modellerinin derinleşmesiyle, optimizasyon avantajları nedeniyle yerini daha pürüzsüz varyantlara (GELU, SwiGLU) bıraktı.
Rönesans: Model boyutlarının büyümesi ve donanım darboğazlarının “işlem”den “belleğe” kaymasıyla, seyreklik (sparsity) özelliği sayesinde tekrar kritik bir önem kazandı.

Geleceğin LLM mimarilerinde, muhtemelen bu yaklaşımların hibrit hallerini göreceğiz. Örneğin, eğitim sırasında pürüzsüz fonksiyonlar (GELU/SwiGLU) kullanıp, çıkarım (inference) aşamasında bunları ReLU’ya dönüştüren veya “Relufication” teknikleriyle sonradan seyrelten yöntemler, hem yüksek zeka kapasitesine hem de düşük enerji maliyetine sahip modellerin anahtarı olacaktır.⁴⁴

Bir bilgisayar bilimci için ReLU, karmaşıklığın içinde sadeliğin gücünü temsil eder. Milyarlarca parametrenin kaotik dünyasında, bir nöronun “susması” (sıfır çıktısı vermesi), bazen konuşması kadar anlamlıdır ve ReLU, yapay zekaya bu “sessizliğin” matematiksel gücünü kazandıran araçtır.