Yapay Zekada Nöroformik Ölçekleme

Gelişmiş Hesaplamalı Mimariler ve Algoritmik Verimlilik: Paralel Temellerden Nöromorfik Ölçekleme Yasalarına1. Giriş: Verimlilik ve Biyolojik Uyumluluğun Yakınsaması

Modern bilgisayar biliminin, özellikle yüksek performanslı hesaplama (HPC) ve yapay zeka alanlarındaki gidişatı, titiz bir verimlilik arayışı ile tanımlanmaktadır. Bu verimlilik arayışı, birbiriyle giderek daha fazla yakınsayan iki eksende gerçekleşmektedir: algoritmik karmaşıklık (bir görev için gereken matematiksel işlemleri optimize etmek) ve donanım kullanımı (bellek hiyerarşileri arasındaki veri hareketini optimize etmek). NASA’da, küresel iklim dinamiklerini modelleyen yerel süper bilgisayar kümelerinden, güneş enerjisiyle çalışan derin uzay sondalarına kadar, görev kritik kısıtlamaların güç ve işlem bütçelerini sınırladığı durumlarda, bu faktörler arasındaki etkileşimi anlamak hayati önem taşır.

Mevcut hesaplama araştırmaları dönemi, Transformer mimarisinin devasa kaba kuvvet paralelliği ile nöromorfik ve tekrarlayan (recurrent) sistemlerin duruma bağlı verimliliği arasındaki gerilimle karakterize edilmektedir. Transformer’lar doğal dil işleme ve bilgisayarlı görü alanlarına hakim olsa da, $O(N^2)$ kuadratik hesaplama karmaşıklığı, telemetri akışları veya yüksek çözünürlüklü gezegen görüntülemesi gibi uzun dizileri işlemek için büyük bir engel teşkil etmektedir.

Bu rapor, bu sınırlamaları ele alan modern hesaplama teorisinin çeşitli ama birbirine bağlı sütunlarını kapsamlı bir şekilde analiz etmektedir. Verimli paralel önek hesaplamalarının temeli olan Blelloch Scan algoritması ile başlıyoruz.¹ Ardından, öğrenmeyi yönlendiren amaç fonksiyonları olarak bilgi teorisinden Çapraz Entropi (Cross-Entropy) ve Enerji Tabanlı Modelleri (EBM’ler) inceliyoruz.³ Analiz, GPU bellek hiyerarşisi kullanımını optimize eden donanım farkındalı bir algoritma olan Flash Attention aracılığıyla derin öğrenmedeki “bellek duvarı” (memory wall) sorununu ele alarak devam ediyor.⁵

Ayrıca, Mamba ⁷ ve RWKV ⁹ gibi Doğrusal Dikkat (Linear Attention) mimarileri aracılığıyla Tekrarlayan Sinir Ağlarının (RNN) yeniden yükselişini ve seçici durum uzaylarını (selective state spaces) keşfediyoruz. Son olarak, Rezervuar Hesaplama ¹¹ ve Hebbian Öğrenme ¹² gibi nöromorfik kavramlar ile DeepMind Chinchilla araştırmasıyla tanımlanan ampirik ölçekleme yasalarını ele alıyoruz.¹³ Bu konuları birleştiren ana tema, statik ve yoğun bellek kullanan mekanizmalardan, donanım farkındalı paralelleştirmeyi kullanan dinamik, $O(N)$ doğrusal karmaşıklıklı modellere geçiştir.

2. Blelloch Scan Algoritması: Paralel Önek Toplamlarının Temelleri

Önek toplamı (prefix sum) veya “scan”, sıralama (radix sort), sözcük analizi, akış sıkıştırma ve polinom değerlendirme gibi işlemler için bir yapı taşı görevi gören temel bir paralel algoritma primitividir. Bir girdi dizisi $A = [x_0, x_1, \dots, x_{n-1}]$ ve bir birleşme operatörü $\oplus$ verildiğinde, scan işlemi $y_i = x_0 \oplus x_1 \oplus \dots \oplus x_i$ (kapsayıcı scan) veya $y_i = x_0 \oplus \dots \oplus x_{i-1}$ (dışlayıcı scan) olacak şekilde bir çıktı dizisi $Y$ hesaplar.

Sıralı bir scan işlemi $O(n)$ süresinde lineer olarak çözülebilirken, bu işlemi paralelleştirmek sezgisel değildir çünkü her çıktı bir önceki çıktının sonucuna bağlıdır; bu da görünüşte katı bir sıralı bağımlılık ima eder. Guy Blelloch tarafından 1990 yılında önerilen algoritma, daha önceki “naif” paralel yaklaşımların verimsizliklerini aşarak iş-verimli (work-efficient) paralel scan işlemleri için standart olmaya devam etmektedir.²

2.1 Algoritmik Karmaşıklık: İş (Work) ve Derinlik (Depth)

Paralel algoritmaları titizlikle değerlendirmek için iki temel karmaşıklık metriğini ayırt etmek gerekir:

• İş ($W$): Algoritma tarafından tüm işlemcilerde yürütülen toplam işlem sayısı. İdeal olarak, bu sıralı karmaşıklıkla eşleşmelidir.
• Derinlik ($D$) (veya Span): Hesaplamadaki en uzun sıralı bağımlılık zinciri (kritik yol). Bu, sonsuz işlemci verildiğinde teorik minimum yürütme süresini belirler.

Hillis-Steele algoritması gibi erken paralel denemeler, logaritmik derinliğe $O(\log n)$ ulaşsa da, $O(n \log n)$ toplama işlemi yaparak iş verimsizliği sorunu yaşamıştır. Bu “iş verimsizliği”, veri elemanlarının sayısı $n$’in fiziksel işlemci sayısı $p$’yi önemli ölçüde aştığı GPU hesaplama senaryolarında kritik bir darboğaz haline gelir. Blelloch scan, toplam işi sıralı algoritmanın karmaşıklığı $O(n)$ ile eşleştiği (sadece sabit bir faktör farkıyla) ve logaritmik derinliği koruduğu için “iş-verimli” olarak adlandırılır.²

Algoritma	İş Karmaşıklığı (Work)	Derinlik Karmaşıklığı (Depth)	Paralel Verimlilik
Sıralı Scan	$O(n)$	$O(n)$	Yok
Naif Paralel (Hillis-Steele)	$O(n \log n)$	$O(\log n)$	Düşük (İş Verimsiz)
Blelloch Scan	$O(n)$	$O(\log n)$	Yüksek (İş Verimli)

2.2 İki Aşamalı Mekanizma

Blelloch algoritması, dizi üzerinde örtük olarak eşlenen dengeli bir ikili ağaç yapısı üzerinde çalışır. Girdi dizisini kavramsal olarak bir ikili ağacın yaprakları olarak ele alır ve iki ayrı aşamada yürütülür: Yukarı Tarama (Up-Sweep/Reduce) ve Aşağı Tarama (Down-Sweep).¹⁷

2.2.1 Aşama 1: Yukarı Tarama (İndirgeme)

Yukarı tarama aşaması, paralel bir indirgeme (reduction) ağacına benzer. Algoritma yapraklardan (girdi dizisi) köke doğru ilerler. Her $d$ adımında, iş parçacıkları bitişik düğümlerin kısmi toplamlarını hesaplar.

• Mantık: Belirli bir derinlik $d$ için ($0$’dan $\log_2 n – 1$’e kadar), işlemler $2^{d+1}$ aralıklarla indeksler üzerinde gerçekleştirilir.
• İşlem: Sağ çocuğun değeri, sol çocuğun toplamını içerecek şekilde güncellenir.
  
  $$x[k + 2^{d+1} – 1] \leftarrow x[k + 2^d – 1] + x[k + 2^{d+1} – 1]$$
• Sonuç: Yukarı taramadan sonra, dizinin son elemanı ($x[n-1]$) tüm elemanların toplamını içerir.¹⁵

2.2.2 Aşama 2: Aşağı Tarama

Aşağı tarama aşaması, Blelloch algoritmasının ayırt edici özelliğidir. Önek toplamlarını hesaplamak için kısmi toplamları ağaçtan aşağıya dağıtır. Dışlayıcı (exclusive) bir scan işlemi yapmak için, önce kök elemanı (yukarı taramada hesaplanan toplam) birim elemana (toplama için 0) ayarlamak gerekir.¹

• Mantık: Kökten ($d = \log_2 n – 1$) 0’a kadar ilerler.
• İşlem: Her düğüm için, değer sol çocuğuna aktarılır; sağ çocuğa ise kendi değeri ile sol çocuğun eski değerinin toplamı aktarılır.
• Formül:
  
  $$t = x[k + 2^d – 1]$$
  (Sol çocuğu sakla)
  
  $$x[k + 2^d – 1] = x[k + 2^{d+1} – 1]$$
  (Sol çocuk ebeveynin değerini alır)
  
  $$x[k + 2^{d+1} – 1] = t + x[k + 2^{d+1} – 1]$$
  (Sağ çocuk = Ebeveyn + Eski Sol)

Bu mantık, tam bir aşağı taramadan sonra her düğümün, ön-sıralı (pre-order) geçişte kendisinden önce gelen tüm yaprak değerlerinin toplamını içermesini sağlar.¹

2.3 Donanım Hususları: Bank Çakışmaları ve Paylaşılan Bellek

Blelloch scan algoritmasının CUDA kullanan Grafik İşlem Birimlerinde (GPU) uygulanması, teorik verimliliği korumak için paylaşılan belleğin (shared memory) dikkatli yönetimini gerektirir. Paylaşılan bellek, ardışık 32-bitlik kelimelerin ardışık banklara atandığı bankalar (modern NVIDIA mimarileri için tipik olarak 32 bank) halinde düzenlenmiştir.¹⁷

Sorun: Adım Kaynaklı Çakışmalar (Stride-Induced Conflicts)

Blelloch scan, geometrik olarak büyüyen ($2^d, 2^{d+1}$ vb.) adımlı bir erişim modeliyle karakterize edilir. Derinlik arttıkça, iş parçacıkları aynı bellek bankasına aynı anda erişmeye çalışabilir. Örneğin $d=5$ olduğunda (adım 32), bir “warp” içindeki tüm iş parçacıkları aynı banka erişmeye çalışır, bu da 32 yollu bir serileştirmeye neden olarak bant genişliğini %96 oranında düşürür.16

Çözüm: Bellek Dolgusu (Memory Padding)

Bunu hafifletmek için geliştiriciler paylaşılan bellek indekslerine dolgu (padding) ekler. Her $M$ kelimede bir (burada $M$ bank sayısıdır) boş bir kelime eklenerek, adım deseni banka eşlemesine göre bozulur. CONFLICT_FREE_OFFSET gibi makrolar kullanılarak bellek adresleri kaydırılır ve çakışmalar ortadan kaldırılarak yüksek verim geri kazanılır.19

Blelloch scan algoritmasının önemi sıralamanın çok ötesine geçer. Bu, Mamba ve diğer modern doğrusal transformer’lardaki Seçici Tarama (Selective Scan) motorudur. Mamba’da tekrarlayan durum güncellemelerini paralelleştirmek için kullanılan “Paralel İlişkisel Tarama”, operatör $\oplus$’nın matris çarpımı olduğu genelleştirilmiş bir Blelloch scan algoritmasıdır.²⁰

3. Makine Öğreniminde Bilgi Teorisi: Çapraz Entropi ve EBM’ler

Bu raporda tartışılan hesaplamalı mimarileri eğitmek için, modelin tahminleri ile gerçeklik arasındaki sapmayı nicelleştiren titiz bir amaç fonksiyonuna ihtiyaç vardır. Sınıflandırma için her yerde bulunan kayıp fonksiyonu olan Çapraz Entropi (Cross-Entropy), Claude Shannon tarafından kurulan bilgi teorisine dayanır.

3.1 Temeller: Entropi ve Sürpriz

Bilgi teorisi, bir olayın bilgi içeriğinin olasılığı ile ters orantılı olduğunu öne sürer. Yüksek olasılıklı bir olay az bilgi taşırken (“sürpriz” azdır), nadir bir olay yüksek bilgi taşır. Olasılığı $p(x)$ olan bir $x$ olayının “sürprizi” veya öz-bilgisi $-\log p(x)$’tir.

Entropi $H(p)$, bir $p(x)$ olasılık dağılımında bulunan beklenen bilgi miktarını (veya belirsizliği) ifade eder:

$$H(p) = \mathbb{E}_{x \sim p}[-\log p(x)] = – \sum_{x} p(x) \log p(x)$$

Deterministik bir dağılım için entropi 0’dır, bu da sıfır belirsizliği yansıtır.4

3.2 Kullback-Leibler (KL) Iraksaması

Gerçek veri dağılımı $P$ ile modelin yaklaşımı $Q$ arasındaki farkı karşılaştırmak için Kullback-Leibler (KL) Iraksamasını kullanırız. $D_{KL}(P |

| Q)$, veri $P$ dağılımından çekildiğinde ancak $Q$ dağılımı kullanılarak kodlandığında “kaybedilen bilgiyi” veya gereken fazladan bitleri ölçer.²³

$$D_{KL}(P |

| Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)} = -H(P) + H(P, Q)$$

Bu türetme kritik bir ilişkiyi ortaya koyar: KL ıraksamasını en aza indirmek (Q’yu P’ye yaklaştırmak), gerçek dağılımın entropisi $H(P)$ sabit kaldığı sürece, $-\sum P(x) \log Q(x)$ terimini en aza indirmeye eşdeğerdir. Gözetimli öğrenmede, $P$ sabit eğitim veri seti tarafından tanımlandığından $H(P)$ sabittir.⁴

3.3 Çapraz Entropi ve Maksimum Olabilirlik Tahmini (MLE)

$H(P, Q) = -\sum_{x} P(x) \log Q(x)$ terimi Çapraz Entropi olarak tanımlanır.

Makine öğrenimi bağlamında, $P(x)$ tipik olarak eğitim verilerinin ampirik dağılımını (genellikle doğru sınıfın olasılığının 1 olduğu one-hot vektör) ve $Q(x)$ modelin tahmin edilen olasılık dağılımını (Softmax çıktısı) temsil eder.

Maksimum Olabilirlik Tahmini (MLE) ile Eşdeğerlik:

Bu toplamı maksimize etmek, matematiksel olarak onun negatifini, yani Negatif Log-Olabilirlik (NLL) değerini minimize etmeye eşdeğerdir. Tek bir eğitim örneği için Çapraz Entropi hesaplaması $-\log Q(c)$’ye (doğru sınıfın log olasılığı) indirgenir. Bu sonuç, o örnek için tam olarak NLL’dir. Dolayısıyla, Çapraz Entropiyi en aza indirmek, model parametreleri altında eğitim verilerinin olabilirliğini (likelihood) maksimize etmekle aynıdır.25

PyTorch gibi çerçevelerde, CrossEntropyLoss sayısal kararlılık için LogSoftmax ve NLLLoss işlemlerini birleştirir (Log-Sum-Exp hilesi).²⁷

3.4 Enerji Tabanlı Modeller (EBM’ler)

Transformatörlerin ve RNN’lerin doğrudan fonksiyon yaklaşımından ayrılan Enerji Tabanlı Modeller (EBM’ler), Yann LeCun tarafından savunulan daha genel bir öğrenme çerçevesi sunar. Normalleştirilmiş bir olasılık dağılımı $P(y|x)$ tahmin etmek yerine, bir EBM her değişken konfigürasyonuna bir skaler “enerji” atayan bir $E(x, y)$ fonksiyonu öğrenir.³

• Düşük Enerji: Uyumlu konfigürasyonlar (örn. doğru etiket).
• Yüksek Enerji: Uyumsuz konfigürasyonlar (örn. yanlış etiket).
• Çıkarım: Tahmin yapmak, enerjiyi en aza indiren $y$’yi bulmaktır: $y^* = \arg\min_{y} E(x, y)$.

Eğitim sırasında, Kontrastif Iraksama (Contrastive Divergence) gibi yöntemler kullanılarak veri noktalarının enerjisi düşürülürken (“push down”), yanlış cevapların enerjisi yükseltilir (“pull up”). EBM’ler, olasılıksal modellerin aksine, tam bölüm fonksiyonunu (partition function) hesaplama zorunluluğunu ortadan kaldırarak mimari esneklik sağlar.²⁹

4. Flash Attention: Bellek Duvarını Aşmak

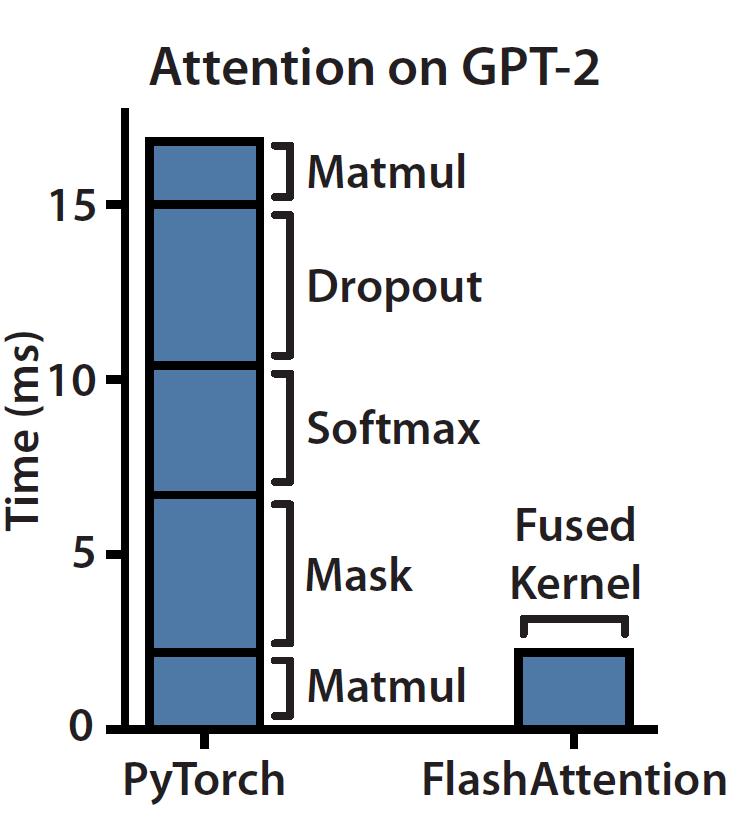
Blelloch scan gibi algoritmik primitifler hesaplamayı optimize ederken, modern derin öğrenme farklı bir darboğazla karşı karşıyadır: bellek bant genişliği. Transformer mimarisinin öz-dikkat (self-attention) mekanizması, $O(N^2)$ zaman ve bellek karmaşıklığı ile bilinir. Ancak, NVIDIA A100 gibi modern GPU’larda darboğaz genellikle aritmetik işlemler (FLOPs) değil, bellek hiyerarşileri arasında veri taşıyan Girdi/Çıktı (IO) işlemleridir. Tri Dao ve ekibi (2022) tarafından tanıtılan Flash Attention, bu donanım sınırlamasını ele alan IO-farkındalı bir kesin dikkat algoritmasıdır.³⁰

4.1 GPU Bellek Hiyerarşisi: HBM ve SRAM

Flash Attention’ın inovasyonunu anlamak için GPU bellek modelini bilmek gerekir:

• HBM (Yüksek Bant Genişlikli Bellek): Ana GPU belleği (örn. 40-80GB). Yüksek kapasiteye ama nispeten düşük bant genişliğine sahiptir.
• SRAM (Statik RAM): Hesaplama birimlerine (Streaming Multiprocessors) fiziksel olarak yakın olan çip üstü bellek (L1 önbellek/Paylaşılan Bellek). Çok küçük kapasiteye (SM başına 192KB) ancak aşırı yüksek bant genişliğine (yaklaşık 19 TB/s) sahiptir.³⁰

Standart dikkat uygulamasında, $N \times N$ boyutundaki devasa dikkat matrisinin HBM’e tekrar tekrar yazılıp okunması birincil darboğazı oluşturur.

4.2 Döşeme (Tiling) ve Çekirdek Birleştirme (Kernel Fusion)

Flash Attention, tam $N \times N$ dikkat matrisini HBM’de oluşturmaktan kaçınmak için Döşeme (Tiling) yöntemini kullanır.

1. Blok Yükleme: Algoritma, Sorgu ($Q$), Anahtar ($K$) ve Değer ($V$) matrislerinin küçük bloklarını HBM’den SRAM’e yükler.
2. Çip Üstü Hesaplama: Dikkat skorlarını doğrudan SRAM içinde hesaplar.
3. Çekirdek Birleştirme: MatMul, Maskeleme, Softmax ve Dropout işlemleri tek bir CUDA çekirdeğinde birleştirilir. Bu, ara sonuçların ana belleğe gidip gelmesini önler.⁶

4.3 Çevrimiçi Softmax (Online Softmax) Hilesi

Softmax fonksiyonu tüm satırın normalizasyonunu gerektirdiğinden, bloklar halinde işlem yapmak zordur. Flash Attention, Çevrimiçi Softmax algoritmasını (Milakov ve Gimelshein) kullanır. Bu teknik, yeni bloklar işlendikçe çalışan maksimum değerin ($m$) ve normalizasyon toplamının ($l$) aşamalı olarak güncellenmesine izin verir.

Güncelleme kuralı, önceki blokların sonucunu yeni maksimum değere göre yeniden ölçeklendirir:

$$O_{new} = diag(l_{new})^{-1} \left( diag(l_{old}) e^{m_{old} – m_{new}} O_{old} + e^{x_j – m_{new}} V_j \right)$$

Bu matematiksel hile, nihai çıktının standart Softmax ile sayısal olarak aynı olmasını sağlarken, işlemin sadece SRAM’de gerçekleşmesine olanak tanır.³² Ayrıca, eğitim sırasında geriye yayılım (backpropagation) için devasa dikkat matrisini saklamak yerine, bu matris yeniden hesaplanır (recomputation). Bu, FLOP sayısını artırsa da, HBM IO’sunu azalttığı için net bir hızlanma sağlar.³¹

5. Transformerları Doğrusallaştırmak: Mamba ve RWKV

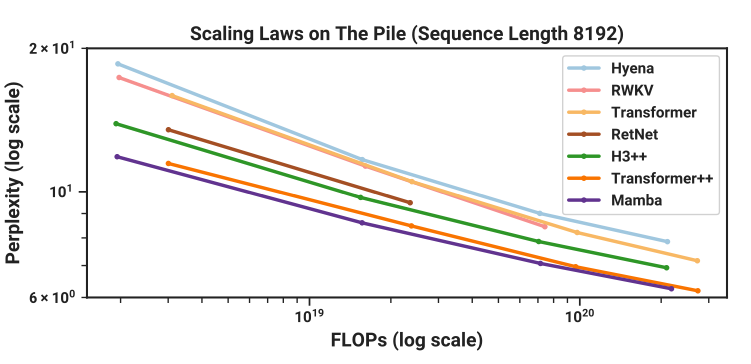
Flash Attention kuadratik Transformer’ı optimize ederken, yeni bir model sınıfı bu kuadratik bağımlılığı tamamen ortadan kaldırmayı ve Tekrarlayan Sinir Ağlarının (RNN) $O(N)$ verimliliğine geri dönmeyi hedefler.

5.1 Durum Uzayı Modelleri (SSM’ler) ve Mamba

Durum Uzayı Modelleri (SSM’ler), kontrol teorisini derin öğrenme ile birleştirir. Sürekli diferansiyel denklemler ayrıklaştırılarak (discretization) metin belirteçlerine (token) uygulanır.

Mamba: Seçici Durum Uzayları

Standart SSM’ler (S4 gibi) Doğrusal Zamanla Değişmeyen (LTI) sistemlerdir. Mamba, parametreleri ($B, C, \Delta$) girdinin bir fonksiyonu yaparak Seçicilik (Selectivity) sunar:

$$B_t = Linear(x_t), \quad C_t = Linear(x_t), \quad \Delta_t = Softplus(Linear(x_t))$$

Bu, sistemin Zamanla Değişen bir yapıya bürünmesini sağlar. Mamba, bu sistemi verimli bir şekilde eğitmek için konvolüsyon yerine Paralel İlişkisel Tarama (Parallel Associative Scan) (Blelloch Scan’in genelleştirilmiş hali) kullanır. Bu algoritma, GPU üzerinde birleştirilmiş (fused) bir çekirdek olarak uygulanır ve uzun dizilerde Transformer’lardan 5 kat daha yüksek çıkarım hızı sağlar.20

5.2 RWKV: Receptance-Weighted Key-Value

RWKV, Transformer gibi eğitilebilen (paralel) ancak RNN gibi çalışan (sabit durum) hibrit bir mimaridir.

Mekanizma:

RWKV, standart $QK^T$ dikkat mekanizmasını, WKV adı verilen doğrusal bir yineleme ile değiştirir.

$$wkv_t = \frac{\sum_{i=1}^{t-1} e^{-(t-1-i)w + k_i} v_i + e^{u+k_t}v_t}{\sum_{i=1}^{t-1} e^{-(t-1-i)w + k_i} + e^{u+k_t}}$$Bu formül, çıkarım (inference) sırasında sabit boyutlu bir duruma (pay ve payda) indirgenebilir:

$$a_t = e^{-w} a_{t-1} + e^{k_t} v_t$$

Bu, RWKV’nin sonsuz bağlam uzunluklarını sabit bellek kullanımıyla işlemesine olanak tanır; bu, Transformer’ların büyüyen KV-önbelleğine (KV-cache) göre büyük bir avantajdır.9

6. Nöromorfik Hesaplama: Rezervuar ve Hebbian Paradigmaları

Biyolojik sistemler, modern yapay zekaya hakim olan geri yayılım (backpropagation) yerine farklı ilkelere dayanır.

6.1 Hebbian Öğrenme ve Oja Kuralı

Donald Hebb’in “Birlikte ateşlenen hücreler, birbirine bağlanır” ilkesi, yerel korelasyonlara dayalı sinaptik plastisiteyi tanımlar. Standart Hebbian öğrenme kararsızdır; ağırlıklar sonsuza kadar büyüyebilir. Oja Kuralı (1982), ağırlık büyümesini dengeleyen bir normalizasyon terimi ekler:

$$\Delta w_i = \eta (x_i y – y^2 w_i)$$

Burada $-y^2 w_i$ terimi, ağırlık vektörünün birim uzunluğa yakınsamasını sağlar ve nöronun girdinin Temel Bileşenini (Principal Component) öğrenmesine olanak tanır.36

BCM Teorisi: Bienenstock-Cooper-Munro teorisi, sinaptik değişim için kayan bir eşik ($\theta_M$) sunarak seçiciliği açıklar. Nöron çok aktifse eşik yükselir (LTP zorlaşır), az aktifse düşer. Bu homeostaz, nöronların farklılaşmasını sağlar.³⁸

6.2 Rezervuar Hesaplama ve Sıvı Durum Makineleri (LSM)

Rezervuar Hesaplama, tekrarlayan ağırlıkları eğitmek yerine sabit tutarak RNN eğitiminin zorluklarını (yok olan gradyanlar) aşar.

• Sıvı Durum Makineleri (LSM): Spiking (Dürtüsel) Sinir Ağları için rezervuar yaklaşımıdır. “Sıvı” (rezervuar), dinamik sinapslara sahip spiking nöronlardan oluşan rastgele bağlı bir havuzdur.
• Ayrıştırma Özelliği (Separation Property): Sıvının farklı girdi akışlarını farklı durum yörüngelerine ayırma yeteneği.
• Yaklaşım Özelliği (Approximation Property): Okuma (readout) katmanının bu durumlardan istenen fonksiyonu oluşturma yeteneği.
  Sadece çıktı (readout) katmanı eğitilir, bu da eğitim maliyetini büyük ölçüde düşürür.40

7. DeepMind Chinchilla: Hesaplama-Optimalliği Çağı

Büyük Dil Modelleri (LLM’ler) alanında odak, saf mimari yenilikten ölçeklemenin ampirik bilimine kaymıştır.

7.1 Kaplan ve Chinchilla Ölçekleme Yasaları

Daha önceki Kaplan (OpenAI) yasaları, performansın en çok parametre sayısı ($N$) ile arttığını öne sürüyordu. Ancak DeepMind’ın Chinchilla araştırması (Hoffmann et al., 2022), 400’den fazla model eğiterek bu görüşü revize etti. Chinchilla, hesaplama-optimal eğitim için parametrelerin ($N$) ve eğitim verisi jetonlarının (token) ($D$) eşit oranda ölçeklenmesi gerektiğini buldu ($N \approx D$).

• Bulgu: Her model boyutu iki katına çıktığında, veri boyutu da iki katına çıkmalıdır. Optimal oran, parametre başına yaklaşık 20 eğitim jetonudur.
• Sonuç: Çoğu model “yetersiz eğitilmişti”. Chinchilla (70B parametre), Gopher’dan (280B) 4 kat daha küçük olmasına rağmen, 4 kat daha fazla veri (1.4 trilyon jeton) ile eğitildiği için daha iyi performans gösterdi.⁴²

7.2 IsoFLOP Eğrileri

Chinchilla araştırmacıları, sabit bir hesaplama bütçesi (FLOPs) için Kayıp (Loss) değerini Model Boyutuna karşı çizerek IsoFLOP eğrilerini oluşturdu. Bu parabolik eğrilerin minimum noktaları, belirli bir bütçe için en verimli model boyutunu gösterir ve modern LLM’lerin (Llama 3 gibi) “veri öncelikli” tasarımını doğrular.⁴⁴

8. Sonuç

Bu rapor, 1990’ların süper bilgisayarları için geliştirilen Blelloch Scan‘in, günümüzde Mamba gibi modellerle lineer zamanlı dizi modellemenin motoru olarak yeniden hayat bulduğunu göstermektedir. Flash Attention, donanım farkındalı optimizasyon ile Transformer’ların bellek darboğazını çözerken; RWKV ve SSM’ler biyolojik verimliliğe daha yakın mimariler sunmaktadır. Chinchilla yasaları ise model boyutlandırmasına ekonomik bir disiplin getirerek verinin önemini vurgulamıştır. NASA için bu gelişmeler, uzay keşfinin katı kısıtlamaları altında hem güçlü hem de sürekli adaptasyon yeteneğine sahip otonom sistemlerin yolunu açmaktadır.

Alıntılanan çalışmalar

1. Prefix Sums and Their Applications – CMU School of Computer Science, erişim tarihi Aralık 10, 2025, https://www.cs.cmu.edu/~guyb/papers/Ble93.pdf
2. Parallel Prefix Sum – Scan, erişim tarihi Aralık 10, 2025, https://www.cs.utexas.edu/~pingali/CS377P/2022fa/lectures/parallelPrefix.pdf
3. A Tutorial on Energy-Based Learning – Yann LeCun, erişim tarihi Aralık 10, 2025, http://yann.lecun.com/exdb/publis/pdf/lecun-06.pdf
4. Cross-entropy – Wikipedia, erişim tarihi Aralık 10, 2025, https://en.wikipedia.org/wiki/Cross-entropy
5. FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness – arXiv, erişim tarihi Aralık 10, 2025, https://arxiv.org/abs/2205.14135
6. From Online Softmax to FlashAttention – Washington, erişim tarihi Aralık 10, 2025, https://courses.cs.washington.edu/courses/cse599m/23sp/notes/flashattn.pdf
7. Mamba: Linear-Time Sequence Modeling with Selective State Spaces – arXiv, erişim tarihi Aralık 10, 2025, https://arxiv.org/html/2312.00752v2
8. From Control Theory to Language Models: Understanding Mamba and State-Space Models | by AnyaB | Medium, erişim tarihi Aralık 10, 2025, https://medium.com/@anyabgm/from-control-theory-to-language-models-understanding-mamba-and-state-space-models-2aa1bed3de05
9. RWKV Architecture: Combining the Power of Transformers and the Efficiency of Recurrent Neural Networks, erişim tarihi Aralık 10, 2025, https://deepfa.ir/en/blog/rwkv-architecture-rnn-transformer-hybrid
10. RWKV Architecture History, erişim tarihi Aralık 10, 2025, https://wiki.rwkv.com/basic/architecture.html
11. [2411.11414] Temporal and Spatial Reservoir Ensembling Techniques for Liquid State Machines – arXiv, erişim tarihi Aralık 10, 2025, https://arxiv.org/abs/2411.11414
12. Oja’s plasticity rule overcomes challenges of training neural networks under biological constraints – arXiv, erişim tarihi Aralık 10, 2025, https://arxiv.org/html/2408.08408v3
13. An empirical analysis of compute-optimal large language model training – Google DeepMind, erişim tarihi Aralık 10, 2025, https://deepmind.google/blog/an-empirical-analysis-of-compute-optimal-large-language-model-training/
14. Chinchilla data-optimal scaling laws: In plain English – LifeArchitect.ai, erişim tarihi Aralık 10, 2025, https://lifearchitect.ai/chinchilla/
15. Parallel Prefix Sum, Scatter and Gather | by Rishabh Khandelwal | Medium, erişim tarihi Aralık 10, 2025, https://rishabh1000khandelwal.medium.com/parallel-prefix-sum-scatter-and-gather-d6d7323c03a1
16. Parallel Prefix Sum (Scan) with CUDA, erişim tarihi Aralık 10, 2025, http://eecs.umich.edu/courses/eecs570/hw/parprefix.pdf
17. Chapter 39. Parallel Prefix Sum (Scan) with CUDA – NVIDIA Developer, erişim tarihi Aralık 10, 2025, https://developer.nvidia.com/gpugems/gpugems3/part-vi-gpu-computing/chapter-39-parallel-prefix-sum-scan-cuda
18. Exclusive Blelloch Scan with Shared Bank Conflict Avoidance Optimization implemented in CUDA – GitHub, erişim tarihi Aralık 10, 2025, https://github.com/p1x31/Blelloch
19. Bank conflict CUDA shared memory? – Stack Overflow, erişim tarihi Aralık 10, 2025, https://stackoverflow.com/questions/28374796/bank-conflict-cuda-shared-memory
20. Here Comes Mamba: The Selective State Space Model | Towards Data Science, erişim tarihi Aralık 10, 2025, https://towardsdatascience.com/here-comes-mamba-the-selective-state-space-model-435e5d17a451/
21. A Visual Guide to Mamba and State Space Models – Maarten Grootendorst, erişim tarihi Aralık 10, 2025, https://www.maartengrootendorst.com/blog/mamba/
22. Information Theory Fundamentals: Entropy, Cross-Entropy, and KL Divergence, erişim tarihi Aralık 10, 2025, https://nimasarang.com/blog/2024-08-24-information-theory/
23. KL Divergence vs Cross Entropy: Exploring the Differences and Use Cases – Medium, erişim tarihi Aralık 10, 2025, https://medium.com/@mrthinger/kl-divergence-vs-cross-entropy-exploring-the-differences-and-use-cases-3f3dee58c452
24. Kullback–Leibler divergence – Wikipedia, erişim tarihi Aralık 10, 2025, https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence
25. A Gentle Introduction to Cross-Entropy for Machine Learning – MachineLearningMastery.com, erişim tarihi Aralık 10, 2025, https://machinelearningmastery.com/cross-entropy-for-machine-learning/
26. Cross-Entropy, Negative Log-Likelihood, and All That Jazz | Towards Data Science, erişim tarihi Aralık 10, 2025, https://towardsdatascience.com/cross-entropy-negative-log-likelihood-and-all-that-jazz-47a95bd2e81/
27. Deriving categorical cross entropy and softmax – Shivam Mehta, erişim tarihi Aralık 10, 2025, https://shivammehta25.github.io/posts/deriving-categorical-cross-entropy-and-softmax/
28. EnergyBased Models: Structured Learning Beyond Likelihoods, erişim tarihi Aralık 10, 2025, http://media.nips.cc/Conferences/2006/Tutorials/Slides/LeCun.pdf
29. A Tutorial on Energy-Based Learning – Stanford University, erişim tarihi Aralık 10, 2025, http://web.stanford.edu/class/cs379c/archive/2012/suggested_reading_list/documents/LeCunetal06.pdf
30. Designing Hardware-Aware Algorithms: FlashAttention | DigitalOcean, erişim tarihi Aralık 10, 2025, https://www.digitalocean.com/community/tutorials/flashattention
31. ELI5: FlashAttention. Step by step explanation of how one of… – Aleksa Gordić, erişim tarihi Aralık 10, 2025, https://gordicaleksa.medium.com/eli5-flash-attention-5c44017022ad
32. Online Softmax to Flash Attention — and Why it Matters | by Matthew Gunton – Medium, erişim tarihi Aralık 10, 2025, https://medium.com/data-science-collective/online-softmax-to-flash-attention-and-why-it-matters-9d676e7c50a8
33. What is Flash Attention? – Biao’s Blog, erişim tarihi Aralık 10, 2025, https://hebiao064.github.io/flash-attn
34. Mamba: Make Sequence Models Fast Again | by Dong-Keon Kim – Medium, erişim tarihi Aralık 10, 2025, https://medium.com/@kdk199604/mamba-make-sequence-models-fast-again-540245a49155
35. How the RWKV language model works | The Good Minima, erişim tarihi Aralık 10, 2025, https://johanwind.github.io/2023/03/23/rwkv_details.html
36. Oja’s rule – Wikipedia, erişim tarihi Aralık 10, 2025, https://en.wikipedia.org/wiki/Oja%27s_rule
37. Unsupervised Hebbian Learning — Neurocomputing | by Amit Yadav – Medium, erişim tarihi Aralık 10, 2025, https://medium.com/@amit25173/unsupervised-hebbian-learning-neurocomputing-55d32aad06df
38. BCM theory – Wikipedia, erişim tarihi Aralık 10, 2025, https://en.wikipedia.org/wiki/BCM_theory
39. BCM theory – Scholarpedia, erişim tarihi Aralık 10, 2025, http://www.scholarpedia.org/article/BCM_theory
40. Neural Simulation Pipeline for Liquid State Machines, erişim tarihi Aralık 10, 2025, https://pja.edu.pl/wp-content/uploads/2023/06/K.Chlasta-PhD-Thesis-NSP-for-LSMs.pdf
41. Enhancing Liquid State Machine Classification Through Reservoir Separability Optimization Using Swarm Intelligence and Multitask Learning – IEEE Xplore, erişim tarihi Aralık 10, 2025, https://ieeexplore.ieee.org/iel8/6287639/10380310/10772455.pdf
42. [2203.15556] Training Compute-Optimal Large Language Models – arXiv, erişim tarihi Aralık 10, 2025, https://arxiv.org/abs/2203.15556
43. Reconciling Kaplan and Chinchilla Scaling Laws – arXiv, erişim tarihi Aralık 10, 2025, https://arxiv.org/html/2406.12907v1
44. CSE 599J: Scaling Laws – Pang Wei Koh, erişim tarihi Aralık 10, 2025, https://koh.pw/cse599j/slides/CSE599J_1-10-24.pdf
45. Thoughts on Chinchilla – irhum.github.io, erişim tarihi Aralık 10, 2025, https://irhum.github.io/blog/chinchilla/

About the Author

Taha Berk Arslan

Administrator

Visit Website View All Posts